Previous chapter: From LTL to Alternating Büchi Automata
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Introduction
The translation from alternating to nondeterministic automata is based on a representation of runs as directed acyclic graphs (DAGs). The idea is similar to the DAG representation we used in the complementation construction for nondeterministic Büchi automata in Section 5.
There the DAG was used to represent the set of all runs of the nondeterministic automaton. The complement automaton would then ”guess” the DAG level-by-level. Here, the DAG is used to represent the branches of a (single) run of the alternating automaton. The idea is illustrated in the following example.
Example
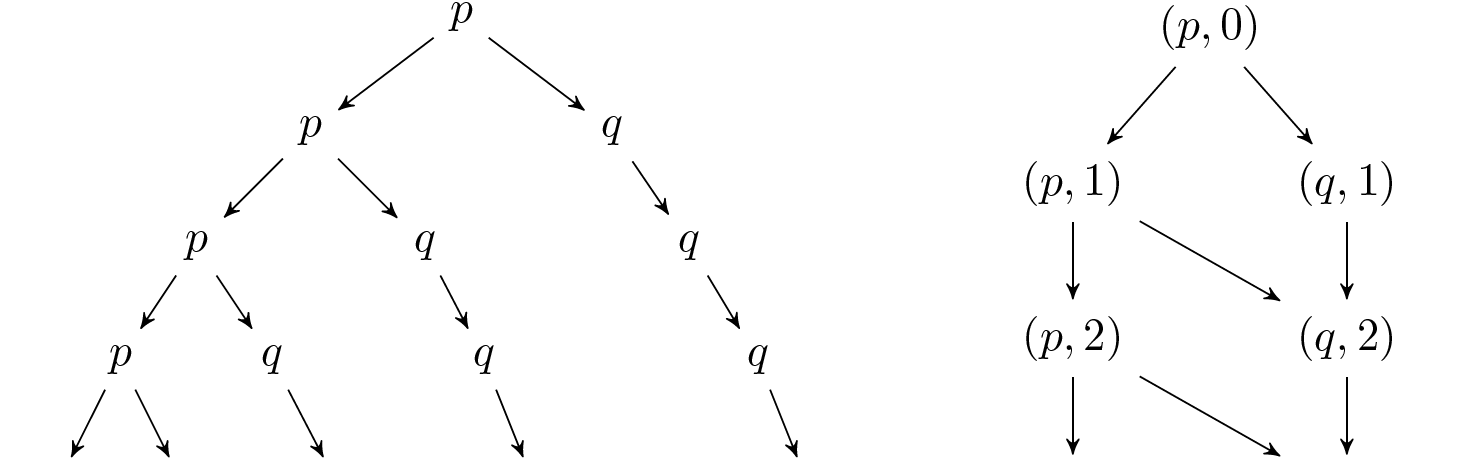
$\textbf{Definition 7.5. } \text{ A } \textit{run DAG }\text{ of an alternating Büchi automaton }\mathcal{A}\text{ on an infinite word }\alpha\text{ is a}\newline\text{DAG }(V,E)\text{, with }V\subseteq Q\times\mathbb{N}\text{ and }(q_0,0)\in V\text{, where}$
$\begin{array}{ll} \hspace{0.5cm} \cdot & E\subseteq \bigcup_{i\in\mathbb{N}}(Q\times\lbrace i\rbrace)\times(Q\times\lbrace i+1\rbrace) \newline \hspace{0.5cm} \cdot & \forall(q,i)\in V \ . \ \exists Y\subseteq Q\text{ s.t. } \newline & Y\models\delta(q,\alpha(i)),Y\times\lbrace i+1\rbrace\subseteq V\text{ and }\lbrace(q,i)\rbrace\times (Y\times\lbrace i+1\rbrace)\subseteq E.\end{array}$
- Every vertices are expressed in (state, letter index)
- Edges are all possible paths from current state $q$
A run DAG is accepting if every infinite path has infinitely many visits to $F\times\mathbb{N}$.
Our construction of the nondeterministic automaton will be based on run DAGs rather than trees.
However, not every run tree can be represented as a DAG. This is illustrated by the following example:
Example (cont.)
The following run tree cannot be represented as a DAG, because there are two nodes that are both labeled with $\mathbf{q}$ has different children (one transits to $p$ and the other to $q$). We say this tree has memory.

Similar Nodes and Memoryless Tree
We call two nodes $x_1, x_2\in\mathcal{T}$ in a run tree $(\mathcal{T},r)$ similar if
- $|x_1| = |x_2|$ (same index), and
- $r(x_1) = r(x_2)$ (same state).
We call a run tree memoryless if the subtrees starting in similar nodes have the same labels.
Memoryless run trees can be represented as DAGs.
$\textbf{Definition 7.5. } \text{ A run tree }(\mathcal{T},r)\text{ is }\textit{memoryless }\text{ if for all similar nodes }x_1\text{ and }x_2\text{ and for all}\newline y\in D^\ast\text{ we have that }(x_1\cdot y\in\mathcal{T}\text{ iff }x_2\cdot y\in\mathcal{T} )\text{ and } r(x_1\cdot y) = r(x_2\cdot y).$
The following theorem shows that whenever there is an accepting run tree, there is also an accepting run tree that is memoryless. Hence, we can show some word are accpeted by the automaton by showing the existence of a memoryless run tree, or, equivalently, the existence of an accepting run DAG.
$\textbf{Theorem 7.2. } \textit{ If an alternating Büchi automaton }\mathcal{A}\textit{ accepts a word }\alpha\textit{, then there exists a}\newline\textit{memoryless accepting run of }\mathcal{A}\textit{ on }\alpha.$
Proof of Memoryless Run exists
Let $(\mathcal{T},r)$ be an accepting run tree on $\alpha$ with directions $D$. We construct a memoryless run tree $(\mathcal{T’},r’)$ by copying from $(\mathcal{T},r)$. Inuitively, we pick, whenever there are multiple occurrences of the same state in $(\mathcal{T},r)$, the occurrence where the last visit to the accepting states was the longest time ago.
$\gamma:\mathcal{T}\rightarrow\mathbb{N}$: number of steps since the last visit to $F$
Initiate the run tree (root) with zero steps:
- $\gamma(\varepsilon)=0$
For $n$’s children $d$, it increase one step from $n$, unless $n$ is an accepting state then it resets to zero
- $\gamma(n\cdot d)=\left\lbrace\begin{array}{ll} \gamma(n)+1 & \text{if }r(n)\notin F\newline 0 & \text{if }r(n)\in F\end{array}\right.$
Now, we can define the tree node that the last visit to the accepting states was the longest time ago based on $\gamma$.
$\Delta:Q\times\mathbb{N}\rightarrow\mathcal{T}$: mapping to return node visit $F$ longest time ago
For state $q\in Q$ and level $n\in\mathbb{N}$, it returns a tree node $y\in\mathcal{T}$ that is the leftmost and visit $F$ longest time ago:
$$\begin{array}{ll}\Delta(q,n)=&\text{the leftmost }y\in\mathcal{T}\text{ with }|y|=n\ \text{ s.t. }\ r(y)=q\newline & \text{and }\forall z\in\mathcal{T}.\ |z|=n\wedge r(z)=q\Rightarrow\gamma(z)\leq\gamma(y)\end{array}$$
Construction of Memoryless Run Tree $(\mathcal{T’},r’)$
We now construct $(\mathcal{T’},r’)$ by copying from the nodes in $(\mathcal{T},r)$ indicated by $\Delta$:
Both trees have same initial states (root):
- $\varepsilon\in\mathcal{T’}\text{ and }r’(\varepsilon)=r(\varepsilon)$
Children node $d$ in $\mathcal{T’}$ are $d$ with longest steps, and of course a child of $n$:
- $d\in\mathcal{T’}\text{ if and only if }\Delta(r’(n),|n|)\cdot d\in\mathcal{T}\text{ and } r’(n\cdot d)=r(\Delta(r’(n),|n|)\cdot d)$
$(\mathcal{T’},r’)$ is a run of $\mathcal{A}$ on $\alpha$
- The root is labeled by the initial state: $r’(\varepsilon)=r(\varepsilon)=q_0$.
- For some node $n\in\mathcal{T’}$, let node $q_n=\Delta(r’(n),|n|)$ ($q_n$ visits $F$ longest time ago among all $n$)
- Then, the set $\lbrace r(q_n\cdot d)\mid d\in D, q_n\cdot d \in \mathcal{T}\rbrace$ satisfies $\delta(r(q_n), \alpha(|q_n|))$ (path of $q_n$ in original tree exists)
- Therefore $\lbrace r’(n\cdot d)\mid d\in D, n\cdot d \in \mathcal{T’}\rbrace\models\delta(r’(n), \alpha(|n|))$ (by the construction above)
$(\mathcal{T’},r’)$ is accepting
First, we show that for every $n\in\mathcal{T’}$, the node obtained from the mapping is indeed the longest path, i.e. $\gamma(n)\leq\gamma(\Delta(r’(n),|n|))$. This is shown by induction on the length of $n$:
for $n=\varepsilon$ we have that $\gamma(n)=0$
for $n=n’\cdot d$ (where $d\in D$) we have:
- if $r(n’)\in F$, then $\gamma(n)=0$
- if $r(n’)\notin F$, then
$$\begin{array}{lcl} \gamma(\Delta(r’(n’\cdot d),|n’\cdot d|))&\overset{\text{Def. }\Delta}{\geq}&\gamma(\Delta(r’(n’),|n’|)\cdot d)\overset{\text{Def. }\gamma}{=}1+\gamma(\Delta(r’(n’),|n’|))\newline&\overset{\text{IH}}{\geq}&1+\gamma(n’)\overset{\text{Def. }\gamma}{=}\gamma(n’\cdot d)\end{array}$$
(Last visit of the Mapping of children of $n’$ $\geq$ Last visit of mapping of $n$’s children. By induction hypothesis, the children of $n’$ through the mapping $\Delta$ is never smaller than any other possible children of $m’$)
Assume $(\mathcal{T’},r’)$ constructed from a accepting $(\mathcal{T},r)$ is not accepting. Then there is an infinite branch that does not visit $F$ infinitely often, i.e. $n_0, n_1, n_2,\dots$ in $\mathcal{T’}$ and $\exists k\in\mathbb{N}$ such that $\forall j\geq k. r’(n_j)\notin F$.
Let $m_i=\Delta(r’(n_i), |n_i|)\text{ for }i\geq k$. We have,
$$
\begin{array}{ccccc} \gamma(n_k)&<&\gamma(n_{k+1})&<&\dots\newline /\mathord{\bigwedge} && /\mathord{\bigwedge}
\newline\gamma(m_k)&<&\gamma(m_{k+1})&<&\dots\end{array}
$$
So, for any $j\geq k$ it holds that $\gamma(m_j)\geq j−k$ (because there are at least $j-k$ steps without visiting $F$). Since $\mathcal{T}$ is finitely branching, there must be a branch with an infinite suffix of non-$F$ labeled positions. So we can always find the branch in $\mathcal{T}$ identical with the path with $m_i$ This contradicts the assumption $(\mathcal{T},r)$ is accepting.
$\textbf{Corollary 7.1. }\textit{A word }\alpha\textit{ is accepted by an alternating Büchi automaton }\mathcal{A}\textit{ if and only if}\newline\mathcal{A}\textit{ has an accepting run DAG on }\alpha$
Translating alternating to nondeterministic automata
We are now ready to translate an alternating Büchi automaton into an equivalent nondeterministic Büchi automaton. The construction is due to Miyano and Hayashi (1984).
$\textbf{Construction 7.2. }\text{For an alternating Büchi automaton }\mathcal{A}=(\Sigma,Q,q_0,\delta,\small\text{BÜCHI} \normalsize(F))\text{, we}\newline\text{construct a nondeterministic Büchi automaton }\mathcal{A’}=(\Sigma,Q’,I’,T’,\small\text{BÜCHI} \normalsize(F’))\text{ with }\mathcal{L(A)}=\newline\mathcal{L(A’)}\text{ as follows:}$
$\begin{array}{ll}
\hspace{0.5cm} \cdot \ Q’&= 2^Q\times2^Q \newline
\hspace{0.5cm} \cdot \ I’&= \lbrace(\lbrace q_0\rbrace,\varnothing)\rbrace\newline
\hspace{0.5cm} \cdot \ T’&= \lbrace((X,\varnothing),\sigma,(X’,X’\setminus F))\mid X’\models\wedge_{q\in X}\delta(q,\sigma)\rbrace\ \cup\newline
&\hspace{0.5cm} \lbrace((X,W),\sigma,(X’,W’\setminus F))\mid W\neq\varnothing,W’\subseteq X’, X’\models\wedge_{q\in X}\delta(q,\sigma),W’\models\wedge_{q\in W}\delta(q,\sigma)\rbrace\newline
\hspace{0.5cm} \cdot \ F’&= \lbrace(X,\varnothing)\mid X\subseteq Q\rbrace
\end{array}$
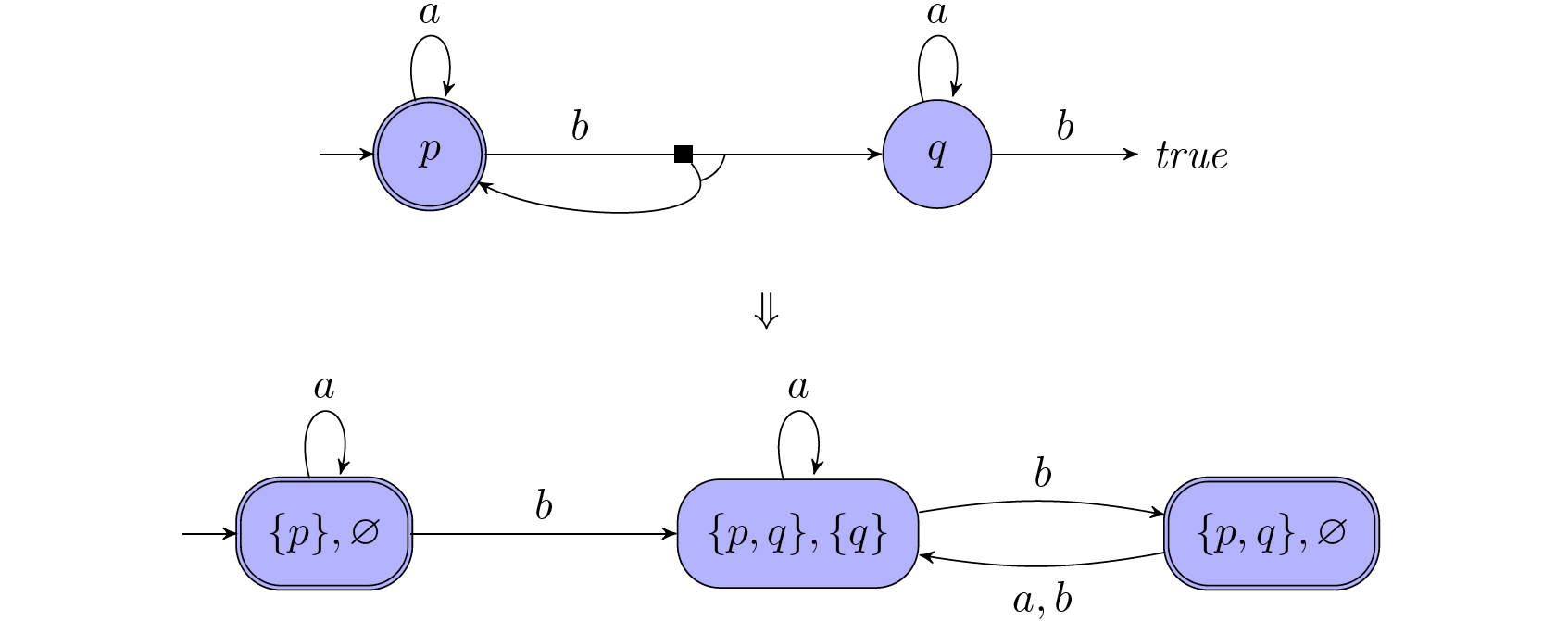
Modified Example from section 7.1

| Example | Explaination | |
|---|---|---|
| $Q’$ | $X=\lbrace\lbrace p\rbrace,\lbrace q\rbrace,\lbrace p,q\rbrace\rbrace$ $W = \lbrace\varnothing,\lbrace q\rbrace\rbrace$ | States Q’ is a tuple consist of two set of states in $Q$, first one must be non-empty and the second one does not contain any states $q\in F$ |
| $I’$ | $I’=(\lbrace p\rbrace,\varnothing)$ | 1st element is the initial state while the second element is empty |
| $T’$ | $(\lbrace p\rbrace,\varnothing)\overset{b}{\longrightarrow}(\lbrace p,q\rbrace,$ $\lbrace \lbrace p,q\rbrace\setminus\lbrace p\rbrace\rbrace)=(\lbrace p,q\rbrace,\lbrace q\rbrace)$ | $X$ represent the behaviour of the original automata, while $W$ tracks whether the original accepting states are visited after the transition. |
| $T’$ | $(\lbrace p,q\rbrace,\lbrace q\rbrace) \overset{b}{\longrightarrow}(\lbrace p,q\rbrace,\varnothing)$ $(\delta(p,b)=p\wedge q,\delta(q,b)=\textit{true}=\varnothing$ $\therefore\delta(p\wedge q,b)=p\wedge q.)$ | If $W$ is empty, it means accepting states is reached and next transition we start again on tracking. If $W$ is non-empty, then its behaviour align with $X$ |
| $F’$ | $F’=\lbrace(\lbrace p\rbrace,\varnothing), (\lbrace p,q\rbrace,\varnothing)\rbrace$ | The run/word is aceepting if $W$ is empty infinite often. |
$\textbf{Theorem 7.3. } \text{(Miyano and Hayashi, 1984). }\textit{For every alternating Büchi automaton }\mathcal{A}\textit{, we can}\newline\textit{effectively construct a nondeterministic Büchi automaton }\mathcal{A’}\textit{ with }\mathcal{L(A)}=\mathcal{L(A’)}.$
Proof
$\mathcal{L(A)}\supseteq\mathcal{L(A’)}$ (all word accepted by $\mathcal{L(A’)}$ must also be accepted by $\mathcal{L(A)}$):
Let $\alpha\in\mathcal{L(A’)}$ with an accepting run $r’=(X_0,W_0)(X_1,W_1)(X_2,W_2)\dots$
where $W_0 =\varnothing$ and $X_0=\lbrace q_0\rbrace$. We construct the run DAG $(V,E)$ for $\mathcal{A}$ on $\alpha$:
All vertices in DAG in level $i$ come from the tree in level $i$:
- $V=\lbrace (x,i)\mid i\in\mathbb{N}, x\in X_i\rbrace$
$X_i$ represent the behaviour of the automaton and $W_i$ is for tracking whether the states are accepting.
If the state is not tracked by $W_i$, i.e. $(x\in X_i \setminus W_i)$, that means it is accepted, no extra tracking is needed,
If it is tracked, i.e. $(x\in W_i)$, it either moves to some accepting state or it is continue tracked $(F\cup W_{i+1})$:- $E=\lbrace((x,i),(x’,i+1))\mid i\in\mathbb{N}, x\in X_i \setminus W_i, x’\in X_{i+1}\rbrace\cup\newline\hspace{0.95cm}\lbrace((x, i),(x’,i+1))\mid i\in\mathbb{N}, x\in W_i, x’\in X_{i+1}\cap (F\cup W_{i+1})\rbrace$
First, we show that $(V,E)$ is a run DAG: $(q_0,0)\in V$ and for every $(x,i)\in V$:
- The state is accepted, any transitions from here are valid:
- if $x\in X_i\setminus W_i,\ X_{i+1}\models\delta(x,\alpha(i))$;
- The state is tracked, only transitions to accepting state or continue tracked are valid:
- if $x\in W_i, x’\in X_{i+1}\cap (F\cup W_{i+1})\models\delta(x,\alpha(i))$.
Since the automata is accepting, so it has $W_i=\varnothing$ exist for infinitely many $i$. So the run DAG is accepting, because there is $x\in X_i\setminus W_i$ infinitely often, every path through the run DAG visits $F$ infinitely often.
$\mathcal{L(A)}\subseteq\mathcal{L(A’)}$ (all word accepted by $\mathcal{L(A)}$ must also be accepted by $\mathcal{L(A’)}$):
Let $\alpha\in\mathcal{L(A)}$ and $(V,E)$ be an accepting run DAG of $\mathcal{A}$ on $\alpha$.
We construct a run $r’=(X_0,W_0)(X_1,W_1)(X_2,W_2)\dots$ on $\mathcal{A’}$ as follows:
$X_0=\lbrace q_0\rbrace$ and $W_0=\varnothing$
We simulate the behaviour using $X_i$: for $i\geq 0$, let $X_{i+1} = \lbrace x’\in Q\mid ((x,i),(x’,i+1))\in E, x\in X_i\rbrace$
- If the state is accepted, align the behaviour with $X$:
$W_{i+1} = X_{i+1} \setminus F$ if $W_i=\varnothing$ - If not, track and see if the accepting condition is fulfiled: $W_{i+1} = \lbrace x’\in Q \setminus F \mid\exists(x,i)\in V, ((x,i),(x’,i+1))\in E,x\in W_i\rbrace$.
- If the state is accepted, align the behaviour with $X$:
Clearly, $r’$ is a run: it starts with $(\lbrace q_0\rbrace,\varnothing)$ and obeys $T’$. That is, $(X_{i+1},W_{i+1})$ contains states in $\delta(x,\alpha(i))$:
- For $x\in X_i\setminus W_i$, we have that $X_{i+1}\models\delta(x,\alpha(i))$;
- For $x\in W_i$, $X_{i+1}\cap (F\cup W_{i+1})$ satisfies $\delta(x,\alpha(i))$.
The run $r’$ is accepting, otherwise some state $(X_{i+1},W_{i+1})$ is rejected, and thus rejects the path in $(V,E)$.
Example with the construction
$\textbf{Corollary 7.2. }\textit{A language is }\omega\textit{-regular if and only if it is recognizable by an alternating Büchi automaton.}$
Summary
In this section, we have proved that any $\omega$-regular language can be recongnized by some alternating Büchi automaton. Let see how it is done.
Every accepted word in an alternating Büchi automaton has an Memoryless Accepting Run (Theorem 7.2).
Every Memoryless Run Tree can be represented as a Run DAG
Thus, Every accepted word in an alternating Büchi automaton has an Accepting Run DAG (Corollary 7.1).
For every Alternating Büchi Automaton there exists a Nondeterministic Büchi Automaton (Theorem 7.3).
An $\omega$-language is Büchi-recognizable iff it is $\omega$-regular (Büchi’s Characterization Theorem) (Theorem 3.6).
An $\omega$-language is Alternating Büchi-recognizable iff it is $\omega$-regular (Corollary 7.2).
Next chapter: Linear Arithmetic (Theory)
Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com