This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Model Checking
Given a system model, we try to check whether it meets its specification automatically and exhaustively.
To describe/represent the system and specification, we use Automata over infinite objects.
Verification Problem
The verification problem can be solved by:
Constructing the intersection of system, with an automaton for the negation of the specification,
then checking whether the language of the resulting automaton is empty.
$\textbf{Example 1.1. } \text{Consider the concurrent program }\small{\text{TURN}}:$
$$\text{local $t$: boolean where initially $t$ = $false$}\newline
P_0::\left[ \begin{array}{l}\text{loop forever do}\newline
\hspace{1cm}\left[ \begin{array}{l}
\ell_0: \text{await }\neg t; \newline
\ell_1: \text{critical;} \newline
\ell_2: t := true; \newline
\end{array} \right]\end{array} \right]
\mid\mid P_1::\left[ \begin{array}{l}
\text{loop forever do}\newline
\hspace{1cm}\left[ \begin{array}{l}
m_0: \text{await } t; \newline
m_1: \text{critical;} \newline
m_2: t := false; \newline
\end{array} \right]\end{array} \right]$$
The example above is a simple solution to the mutual exclusion problem:
it ensures that at any given point of time, at most one process is in the critical region.
From Program to automaton
To represent the above program using automaton, we need to define an alphabet $\Sigma$.
Firstly, we fix a set of atomic propositions (AP), that is (potentially) relevant to the program states.
For the program in $\small{\text{Example 1.1}}$, $AP = \lbrace\ell_0,\ell_1,\ell_2,m_0,m_1,m_2,t\rbrace$.
i.e. The present program location and the current value of $t$.
Then, we define the alphabet as $\Sigma = 2^{AP}$, the set of subsets of $AP$.
An $AP$ is included in the subset if it is currently $true$.

This automaton is a safety automaton, it accepts all infinite repetitons of the sequence
$\lbrace\ell_0,m_0\rbrace \lbrace\ell_1,m_0\rbrace \lbrace\ell_2,m_0\rbrace \lbrace\ell_0,m_0,t\rbrace \lbrace\ell_0,m_2,t\rbrace$
Automata Verification
To verify $\small{\text{TURN}}$ satisfies the mutual exclusion property ($P_0$ and $P_1$ are never in $\ell_1$ and $m_1$ at the same time),
we build an automaton that represents the negation (eventually $P_0$ and $P_1$ are simultaneously in location 01):
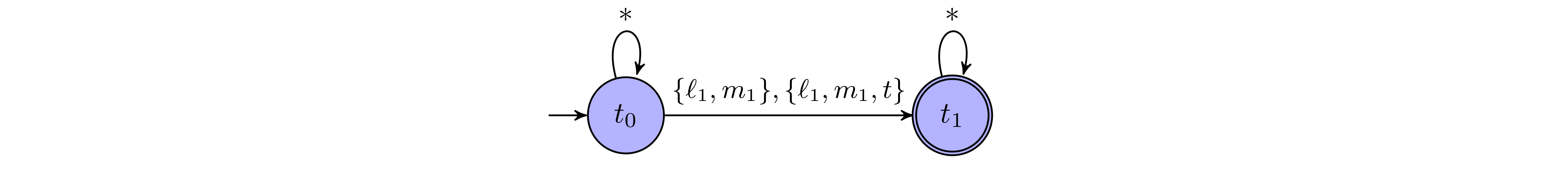
This automaton is a Büchi automaton with accepting state $t_1$.
A word is accepted if $t_1$ is visited infinitely often.
For every word accepted by the system automaton, this property automaton stays in $t_0$ forever and therefore does not accept the word.
This means there does not exist an infinite sequence that generated by the program, and
accepted by the negation automaton of the specification. In other words, $\small{\text{TURN}}$ is correct.
Next post: Synthesis
Further Reading: Büchi automaton
Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com