Previous chapter: Model Checking
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Synthesis
In synthesis, we check automatically if there exists a program that satisfies a given specification.
If the answer is yes, we construct such a program.
We solve it by determine the winner of a two-player game between a system player and an environment player.
| Task | Goal | |
|---|---|---|
| System player | choose the outputs of the system | meet the specification |
| Environment player | choose the inputs of the system | falsify the specification |
Therefore, the specification is satisfied if the System player wins.
Such winning strategy can be translated into a program that is guaranteed to satisfy the specification.
Example: coffee machine
In this example, we assume there’s a machine that “outputs coffee” whenever users press a button.
Set of $AP = \lbrace bu, co\rbrace$, where input $AP_I = \lbrace bu\rbrace$ and output $AP_O = \lbrace co\rbrace$.
Specification: $co$ should hold iff. $bu$ holds in every step.
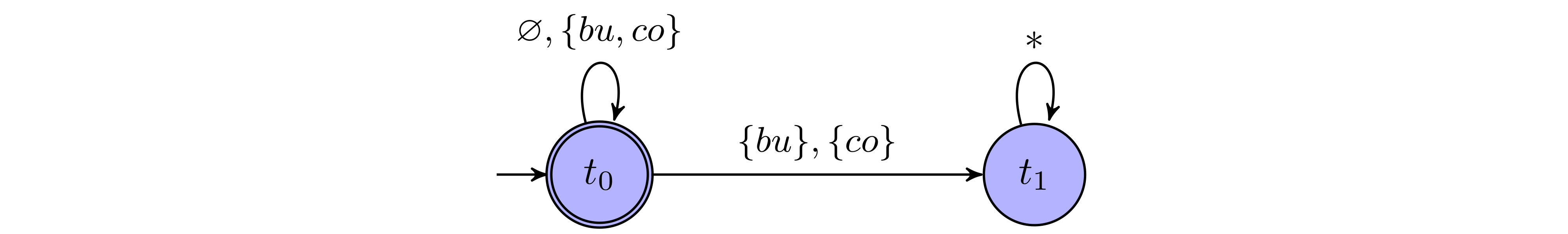
From this automaton, we construct a game arena where in each round,
- Environment player chooses the input ($bu$ or $\neg bu$)
- System player chooses the output ($co$ or $\neg co$)
States of the game keep track of the corresponding state of the automaton,
then we can determine who is the winner for each possible play.
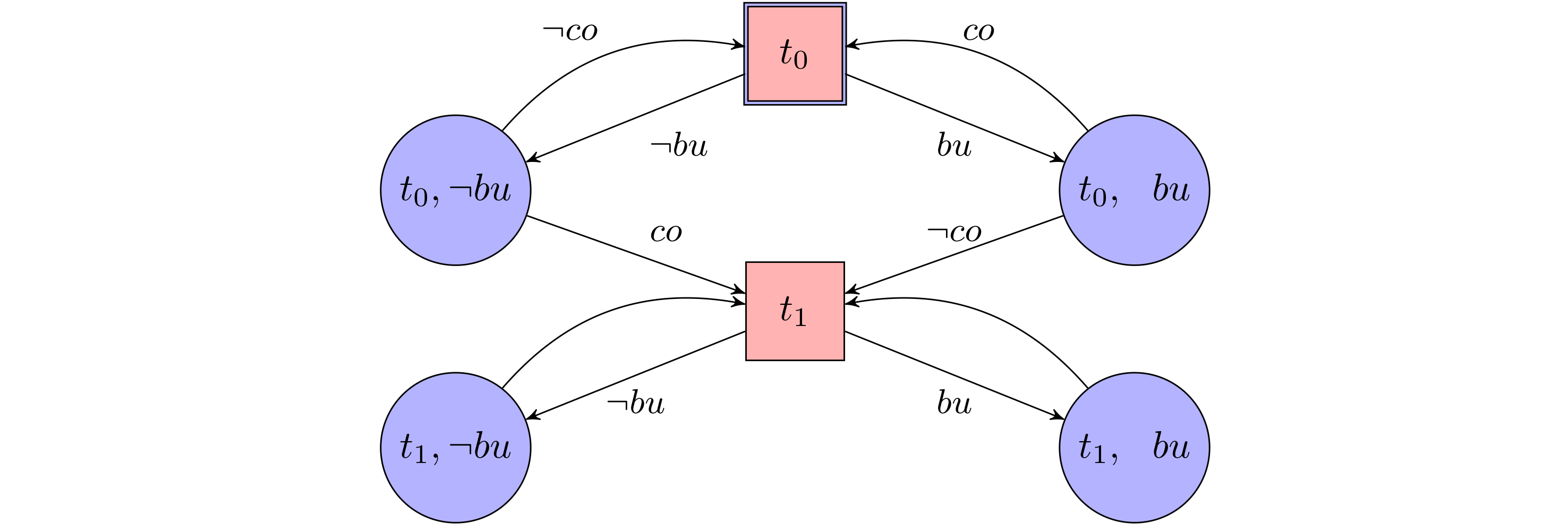
Here, system player gets to choose the next move with circles, and environment player choose with squares.
System player has a simple winning strategy from starting position $t_0$:
react input $bu$ with output $co$, and react input $\neg bu$ with output $\neg co$
In this way, the play visits $t_0$ infinitely often, which proves that it satisfies the specification.
Next chapter: The Logic-Automata Connection
Further Reading: Program synthesis
Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com