Previous chapter: Closure Properties of Muller automata Under Boolean Operations
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Introduction
To prove McNaughton’s theorem, in this subsection, we will introdue the semi-deterministic Büchi automata.
- translate nondeterministic Büchi automata into semi-deterministic Büchi automata.
- translate from semi-deterministic Büchi automata to deterministic Muller automata.
Semi-deterministic Büchi Automata
A semi-deterministic automaton is a (possibly nondeterministic) automaton where all accepting runs ultimately end up in a subset of the states from which all transitions are deterministic.
$\textbf{Definition 10.2. } \text{A Büchi automata }\mathcal{A} = (\Sigma,Q,I,T,\small\text{BÜCHI} \normalsize(F))\text{ is }\textit{semi-deterministic}\text{ if}\newline Q = N \uplus D\text{ is a partition of }Q\text{ such that }F\subseteq D, pr_2(T\cap(D\times\Sigma\times Q))\subseteq D\text{, and }\newline(\Sigma,D,\lbrace d\rbrace,T\cap(D\times\Sigma\times D),\small\text{BÜCHI}\normalsize(F)) \text{ is deterministic for every }d\in D.$
Explaination
$Q = N \uplus D:$ a disjoint union symbol $\uplus$ indicates that $N$ and $D$ are two seperated subset.
$D:$ firstly, set of accepting states in part of $D$ ($F\subseteq D$). Then for all transistion starts from $D$ ($T\cap(D\times\Sigma\times Q)$), their successors are also in $D$ ($pr_2(T\cap(D\times\Sigma\times Q))\subseteq D$).
Therefore, we can split such automaton into nondeterministic part $N$ and determinstic part $D$, and the accepting run will end up stays in $D$.
From Nondeterministic to Semi-deterministic Büchi Automata
The translation is based on a subset construction, where we collect two sets of states:
- the states that are reachable on the given input word, and
- the states that are reachable on some path through an accepting state.
A state of the semi-deterministic automaton is accepting if the two sets become equal; when this happens, the second set is reinitialized with the subset of accepting states that appear in the first component.
Example
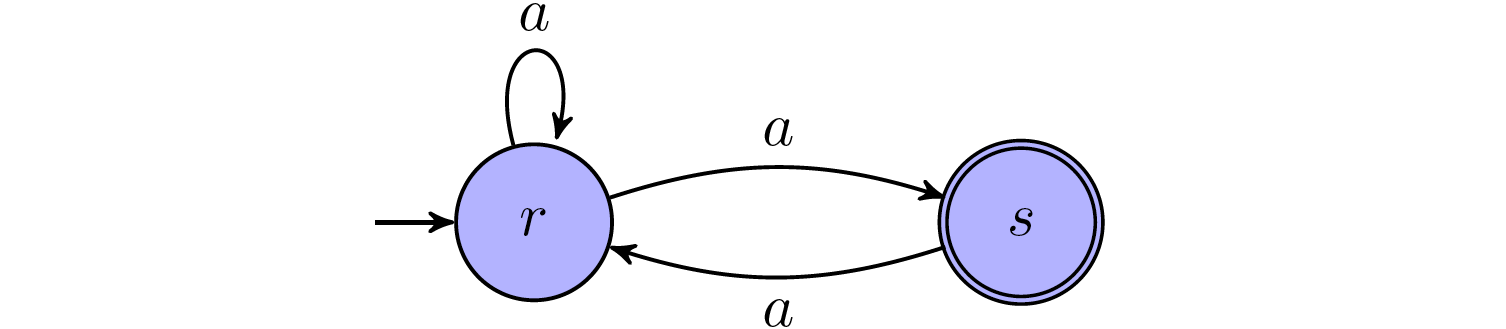

The subset construction produces a deterministic automaton that accepts a subset of the words accepted by the original automaton. If the two sets are equal infinitely often, we can construct a run of the original automaton that goes through accepting states infinitely often:
intuitively, we can go “backwards” from each position where the two sets have become equal and select a path segment for the original automaton where an accepting state is visited (in the proof below we give a more precise argument using König’s lemma).
There is no general guarantee that the set of reachable states from some position of an accepting run and the set of states reachable on a path through some accepting state are the same. This is illustrated by the following example.
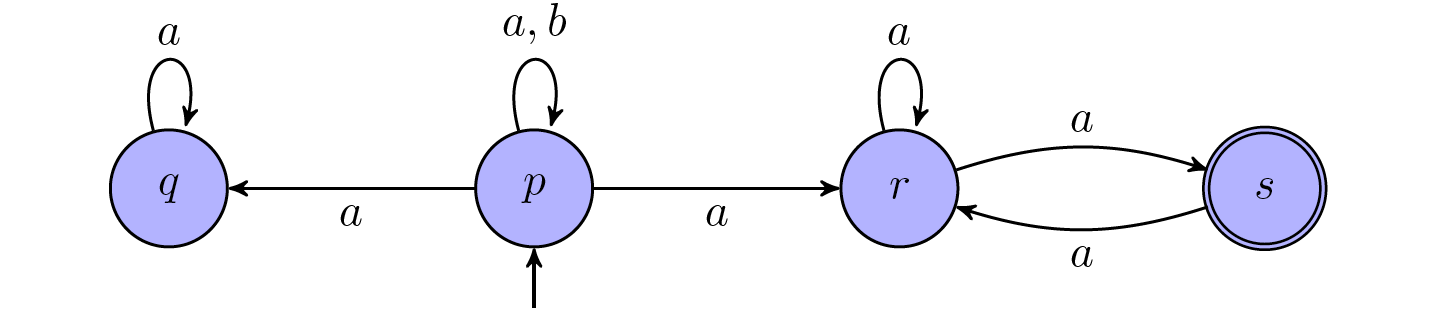
Let the input word be $\alpha^\omega$. From the initial position of some run, which starts in the initial state $p$, all states are reachable, but only $r$ and $s$ are reachable on paths from $s$.
Ultimately, however, every accepting run must reach (and remain in) positions where the set of reachable states and the set of states reachable on a path through some accepting state are the same. This is because the set of reachable states can only become smaller finitely often; hence, at some point, the set of reachable states will remain the same from all subsequent positions, including those (future) positions of the accepting run where the run visits an accepting state.
In our semi-deterministic automaton, we therefore start by simulating the given nondeterministic automaton. At any point we allow a nondeterministic transition into the (from then on) deterministic subset construction.
$\textbf{Construction 10.5. } \text{For a Büchi automaton }\mathcal{A}=(\Sigma,Q,I,T,\small\text{BÜCHI}\normalsize (F))\text{, we construct the semi-}\newline\text{deterministic Büchi automaton }\mathcal{A’} = (\Sigma,Q’,I’,T’,\small\text{BÜCHI}\normalsize (F’))\text{ with }\mathcal{L}(\mathcal{A’})=\mathcal{L}(\mathcal{A})\text{ as follows:}$
$\begin{array}{l}
\hspace{1cm} \cdot \ Q’=Q\uplus (2^Q\times2^Q)\newline
\hspace{1cm} \cdot \ I’=I’ \newline
\hspace{1cm} \cdot \ T’=T\cup\lbrace(q,\sigma,(\lbrace q’\rbrace,\varnothing))\mid(q,\sigma,q’)\in T\rbrace \newline
\hspace{2.85cm}\cup \ \lbrace((L_1,L_2),\sigma,(L’_1,L’_2))\mid L_1\neq L_2\newline
\hspace{3.8cm}L’_1=pr_2(T\cap L_1\times\lbrace\sigma\rbrace\times Q)\newline
\hspace{3.8cm}L’_2=pr_2(T\cap L_1\times\lbrace\sigma\rbrace\times F)\cup pr_2(T\cap L_2\times\lbrace\sigma\rbrace\times Q)\rbrace\newline
\hspace{2.85cm}\cup \ \lbrace((L_1,L_2),\sigma,(L’_1,L’_2))\mid L_1= L_2\newline
\hspace{3.8cm}L’_1=pr_2(T\cap L_1\times\lbrace\sigma\rbrace\times Q)\newline
\hspace{3.8cm}L’_2=pr_2(T\cap L_1\times\lbrace\sigma\rbrace\times F)\newline
\hspace{1cm} \cdot \ F’=\lbrace(L,L)\in(2^Q\times2^Q)\mid L\neq\varnothing\rbrace\newline
\end{array}$
$\textbf{Lemma 10.1. } \textit{For every Büchi automaton }\mathcal{A}\textit{ there exists a semi-deterministic Büchi}\newline\textit{automaton }\mathcal{A’}\textit{ with }\mathcal{L}(\mathcal{A})=\mathcal{L}(\mathcal{A’}).$
Proof
$\mathcal{L}(\mathcal{A’})\subseteq\mathcal{L}(\mathcal{A})$
Let $\alpha\in\mathcal{L}(\mathcal{A’})$ and let $r’=q_0q_1\dots q_{n-1}(L_n,L’n)(L{n+1},L’{n+1})\dots$ be an accepting run of $\mathcal{A’}$ on $\alpha$. Since $r’$ is accepting, there is an infinite sequence $i_0i_1\dots$ of indices such that $i_0=n$, and, for all $j\geq1$, $L{i_j} = L’{i_j}$ and $L’{i_j}\neq\varnothing$. For every $j\geq1$, and every $q’\in L_{i_j}$ there exists a state $q\in L_{i_{j−1}}$ and a sequence $q = q_{i_{j−1}} , q_{i_{j−1}+1},\dots, q_{i_j} = q’$ such that $(q_k, \alpha(k), q_{k+1})\in T$ for all $k\in \lbrace i_{j−1},\dots,i_j − 1\rbrace$ and $q_k\in F$ for some $k\in\lbrace i_{j−1}+1,\dots,i_j\rbrace$. We use the following notation: $\textit{predecessor}(q’,i_j) := q, \textit{run}(q’,i_0) = q_0q_1\dots q_{n−1}q’$ for $L_{i_0} = \lbrace q’\rbrace$, and $\textit{run}(q’,i_j)=(q_{i_{j−1}+1})(q_{i_{j−1}+2})\dots q_{i_j}$, for $j\geq1$.
Now consider the j∈N Lij × {j} -labeled tree where the root is labeled with (q ′ , 0) for Li0 = {q ′}, and the parent of each node with a label (q ′ , j) is labeled with (predecessor(q ′ , ij ), j − 1). The tree is infinite and finite-branching, and, hence, by K¨onig’s Lemma, has an infinite branch (qi0 , i0),(qi1 , i1), . . ., corresponding to an accepting run of A: run(qi0 , i0) · run(qi1 , i1) · run(qi2 , i2) · . . .
L(A) ⊆ L(A′ ): Let α ∈ L(A) and let r = q0, q1, . . . be an accepting run of A on α. Let i ∈ N be an index s.t. qi ∈ F and for all j ≥ i there exists a k > j, such that {q ∈ Q | qi α[i,k] −−−→ q} = {q ∈ Q | qj α[j,k] −−−→ q}. The index i exists: ”⊇” holds for all i, because there is a path through qj . Assume, by way of contradiction, that for all i ∈ N, there is a j ≥ i s.t for all k > j ”⊋” holds. Then there exists an i ′ s.t. {q ∈ Q | qi ′ α[i ′ ,k] −−−−→ q} = ∅ for all k > i′ . Contradiction. We define a run r ′ of A′ : r ′ = q0 . . . qi−1({qi}, ∅)(L1, L′ 1 )(L2, L′ 2 ). . . where Lj and L ′ j are determined by the definition of A′ . To prove that r ′ is accepting, assume otherwise, and let m ∈ N be an index such that Ln ̸= L ′ n for all n ≥ m. Then, let j > m be some index with qj ∈ F; hence qj ∈ L ′ j . There exists a k > j such that L ′ k+1 = {q ∈ Q | qj α[j,k] −−−→ q} = {q ∈ Q | qi α[i,k] −−−→ q} = Lk+1. Contradiction.
Next chapter: From semi-deterministic Büchi to deterministic Muller
Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com