Previous chapter: Infinite Games (Basic Definitions)
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Reachability Condition
We will now analyze infinite games for various types of winning conditions. We start with the simple reachability condition.
The reachability condition is given as a set $R$ of positions called the reachability set. The reachability condition is satisfied if the play reaches some position in $R$. Formally, for an infinite word $\alpha$ over $\Sigma$, we use $\text{Occ}(\alpha) := \lbrace\sigma\in\Sigma\mid\exists n\in\mathbb{N}.\ \alpha(n)=\sigma\rbrace$ to denote the set of all letters occurring in $\alpha$.
$\textbf{Definition 11.11. } \text{The }\textit{reachability condition }\small\text{REACH} \normalsize(R)\text{ on a set of positions }R\subseteq V\text{ is the set}$
$$\small\text{REACH} \normalsize(R) = \lbrace\rho\in V^\omega\mid\text{Occ}(\rho)\cap R\neq\varnothing\rbrace\newline\newline\text{A game }\mathcal{G}=(\mathcal{A},\text{Win})\text{ with Win}=\small\text{REACH} \normalsize(R)\text{ is called a }\textit{reachability game}\text{ with reachability set }R$$
Example
$$\text{Position of Player 0: Circles;}\ \ \text{Positions of Player 1: rectangles.}$$
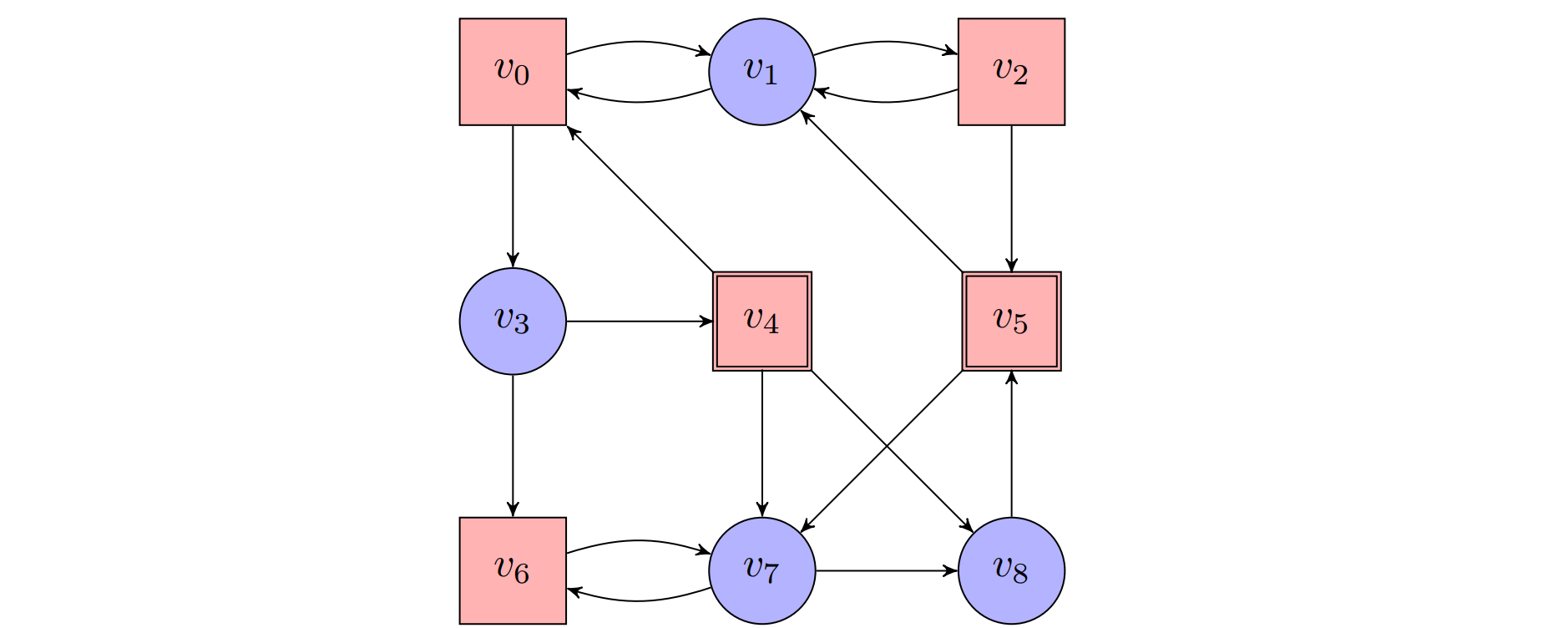
$$\mathcal{G}=(\mathcal{A},\small\text{REACH} \normalsize(R)),\ R=\lbrace v_4,v_5\rbrace$$
- The winning region for Player 0: $W_0(\mathcal{G})=\lbrace v_3,v_4,v_5,v_6,v_7,v_8\rbrace$
- Strategy: $\sigma(v_1) = v_2, \sigma(v_3) = v_4, \sigma(v_7) = v_8, \sigma(v_8) = v_5$
Attractor Construction
Reachability games can be solved with a simple fixed point construction called the attractor construction.
The attractor construction computes the winning region for Player 0 iteratively by the reachability set:
adds all positions owned by Player 0 that have an edge into the winning region,
then adds all positions owned by Player 1 where all edges lead into the winning region. (no choices)
Repeats until no more positions can be added.
In the following, we give a slightly more general definition of the attractor construction that can be applied also to Player 1. We do this in preparation for the constructions for other winning conditions, which will use the attractor construction as a subroutine.
$\textbf{Construction 11.1. } \text{Let an arena }\mathcal{A} = (V,V_0,V_1,E)\text{ be given. The }\textit{attractor construction}\text{ on}\newline\mathcal{A}\text{ is defined for each Player }i\text{, for all }n\in\mathbb{N}\text{ and }R\subseteq V\text{ as follows.}$
$\begin{array}{lll}
\hspace{1cm} \cdot \ CPre^{i}(R) &=& \lbrace v\in V_i\mid\exists v’\in V.(v, v’)\in E\wedge v’\in R\rbrace\cup\ \newline
&&\lbrace v\in V_{1-i}\mid\forall v’\in V.(v, v’)\in E\rightarrow v’\in R\rbrace\newline
\hspace{1cm} \cdot \ Attr_{0}^{i}(R)&=&R \newline
\hspace{1cm} \cdot \ Attr_{n+1}^{i}(R)&=&Attr_{n}^{i}(R)\cup CPre^{i}(Attr_{n}^{i}(R)) \newline
\hspace{1cm} \cdot \ Attr^{i}(R)&=&\underset{n\in\mathbb{N}}{\bigcup} Attr_{n}^{i}(R)\newline
\end{array}$
Example
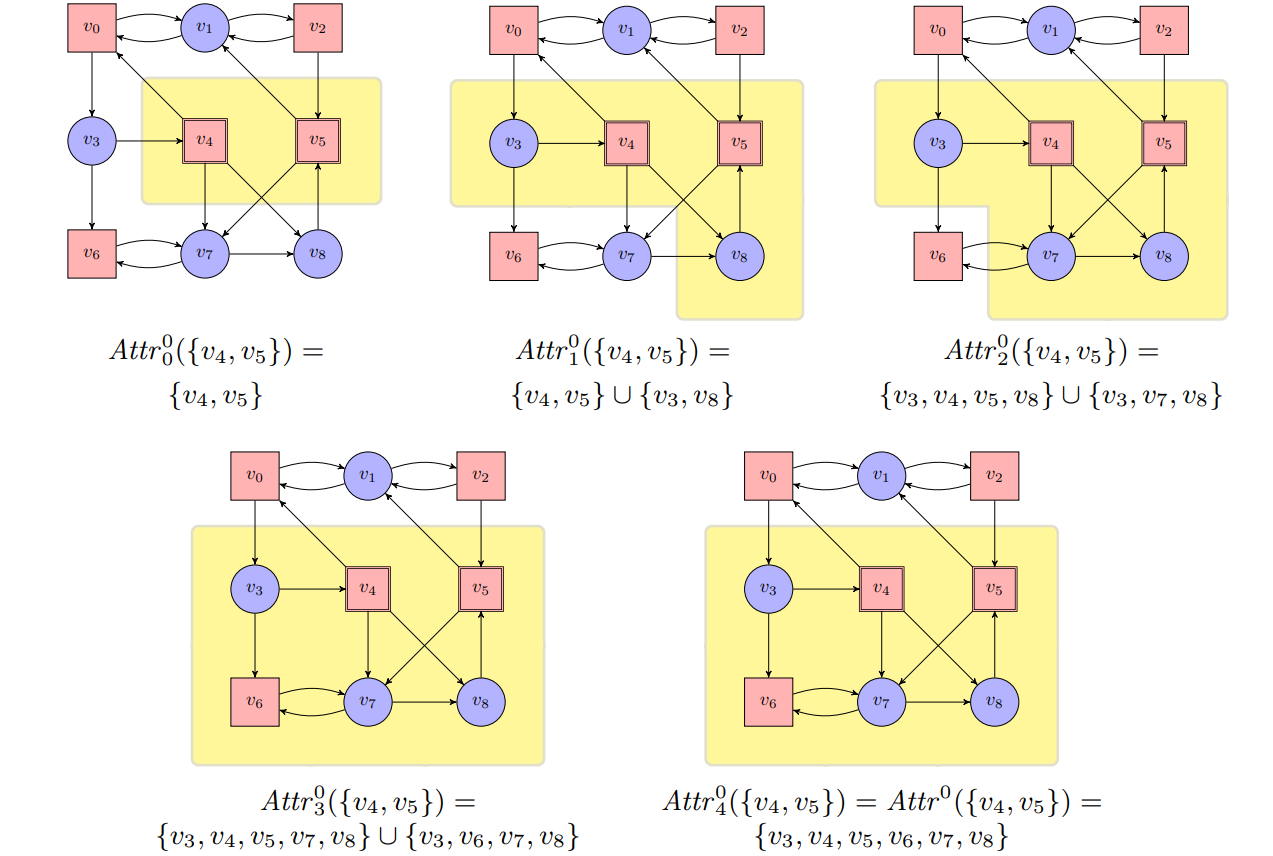
In general, the attractor construction solves a game with winning condition $\small\text{REACH} \normalsize(R)$ as follows: $W_0(\mathcal{G})=Attr^0(R), W_1(\mathcal{G})=V\setminus W_0(\mathcal{G})$. We can furthermore give a uniform memoryless winning strategy. These results are summarized in the following theorem.
$\textbf{Theorem 11.1. } \textit{Reachability games are memoryless determined. It holds that}\newline W_0(\mathcal{G})=Attr^0(R), W_1(\mathcal{G})=V\setminus W_0(\mathcal{G})\textit{. Both players have a uniform winning strategy.}$
Proof
We show for all positions $v\in V$ that
If $v\in Attr^0(R)$, then $v\in W_0(\mathcal{G})$, with the following uniform memoryless strategy $\sigma$:
We fix an arbitrary total ordering on $V$ . For $v\in (Attr^0(R)\setminus R)\cap V_0$, let $n = min\lbrace n\in\mathbb{N}\mid v\in Attr_{n}^0(R)\rbrace$. Then, let $\sigma(v)$ be the smallest $v’\in Attr_{n-1}^0(R)$ with $(v, v′)\in E$
For every other position $v\in V_0\setminus(Attr^0(R)\setminus R)$, let $\sigma(v)$ be the smallest $v’\in V$ with $(v, v′)\in E$
We show, by induction on $n\in\mathbb{N}$, that any play that starts in $v\in Attr_{n}^0(R)$
and is consistent with $\sigma$ reaches $R$ within at most $n$ steps.
If $v\in V\setminus Attr^0(R)$, then $v\in W_1(\mathcal{G})$, with the following uniform memoryless strategy $\tau$:
We again fix an arbitrary total ordering on $V$. For $v\in V_1\setminus Attr^0(R)$, let $\tau(v)$ be the smallest $v’\in V\setminus Attr^0(R)$ such that $(v, v′)\in E$. Such a successor $v’$ always exists, because otherwise $v\in Attr^0(R)$.
For every other position $v\in V_1\cap Attr^0(R)$ let $\tau(v)$ be the smallest $v’\in V\setminus Attr^0(R)$ with $(v, v′)\in E$. Now let $\rho$ be an arbitrary play that is consistent with $\tau$.
We show, by induction on $n$, that $\rho(n)\notin Attr^0(R)$ and, hence, $\rho(n)\notin R$, for all $n\in\mathbb{N}$.
Explaination
Strategy for Player 0
If a position $v$ belongs to $Attr_{n}^0(R)\setminus R$, it must have edges to $v’\in Attr_{n-1}^0(R)$, then choose the smallest $v’$
If a position $v$ does not belong to $Attr^0(R)\setminus R$, simply choose the smallest $v’$ from its edges.
Strategy for Player 1
If a position $v$ does not belong to $Attr_{n}^0(R)$, it must have any one edge does not move to $Attr^0(R)$, choose the smallest $v’$ among those.
If a position $v$ belongs to $Attr_{n}^0(R)$, since all its edges move to some positions in $Attr_{n}^0(R)$, simply choose the smallest $v’$ from its edges.
Next chapter: Büchi Games
Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com