Previous chapter: Reachability Games
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Recurrence Construction
In a Büchi game, the goal of Player 0 is to visit some accepting position infinitely often. The attractor construction allows us to check whether there is a strategy which enforces at least one visit to an accepting position.
Winning a Büchi game is more difficult. Reaching an accepting state at least once is indeed a necessary precondition, but we also have to ensure that from this position we can enforce a second visit to some accepting state, then a third, and so forth. The recurrence construction computes the largest subset of the accepting states from which Player 0 can enforce infinitely many subsequent visits to the subset.
$\textbf{Construction 11.2. } \text{Let an arena }\mathcal{A} = (V_0,V_1,E)\text{ with }V=V_0\cup V_1\text{ be given. The }\newline\textit{recurrence construction}\text{ on }\mathcal{A}\text{ is defined for all }n\in\mathbb{N}\text{ and }F\subseteq V\text{ as:}$
$\begin{array}{lll}
\hspace{1cm} \cdot \ W_n^1(F) &=& V\setminus Attr^0(Recur_n(F))\newline
\hspace{1cm} \cdot \ Recur_{0}(F)&=&F \newline
\hspace{1cm} \cdot \ Recur_{n+1}(F)&=&Recur_{n}(F)\setminus CPre^{1}(W_n^1(F)) \newline
\hspace{1cm} \cdot \ Recur(F)&=&\underset{n\in\mathbb{N}}{\bigcap} Recur_{n}(R)\newline
\end{array}$
The set $W_n^1(F)$ contains those positions in $V$ from which Player 1 can enforce that at most $n$ visits to $F$.
The set $CPre^{1}(W_n^1(F))$ adds those positions in $V$ from which move to positions in $W_n^1(F)$, meaning that there are at most $n+1$ visits to $F$ in newly added positions.
The set $Recur_{n}(F)$ contains the subset of $F$ from which Player 0 can enforce at least $n$ further (i.e., a total of at least $n+1$) visits to $F$.
The set $Recur(F)$ contains the subset of $F$ from which Player 0 can enforce infinitely many visits to $F$. The recurrence construction solves a game with winning condition $\small\text{BÜCHI} \normalsize (F)$ as follows:
$$W_0(\mathcal{G})=Attr^0(Recur(F)),\ W_1(\mathcal{G})=V\setminus W_0(\mathcal{G})$$
$$\text{Position of Player 0: Circles;}\ \ \text{Positions of Player 1: rectangles.}$$
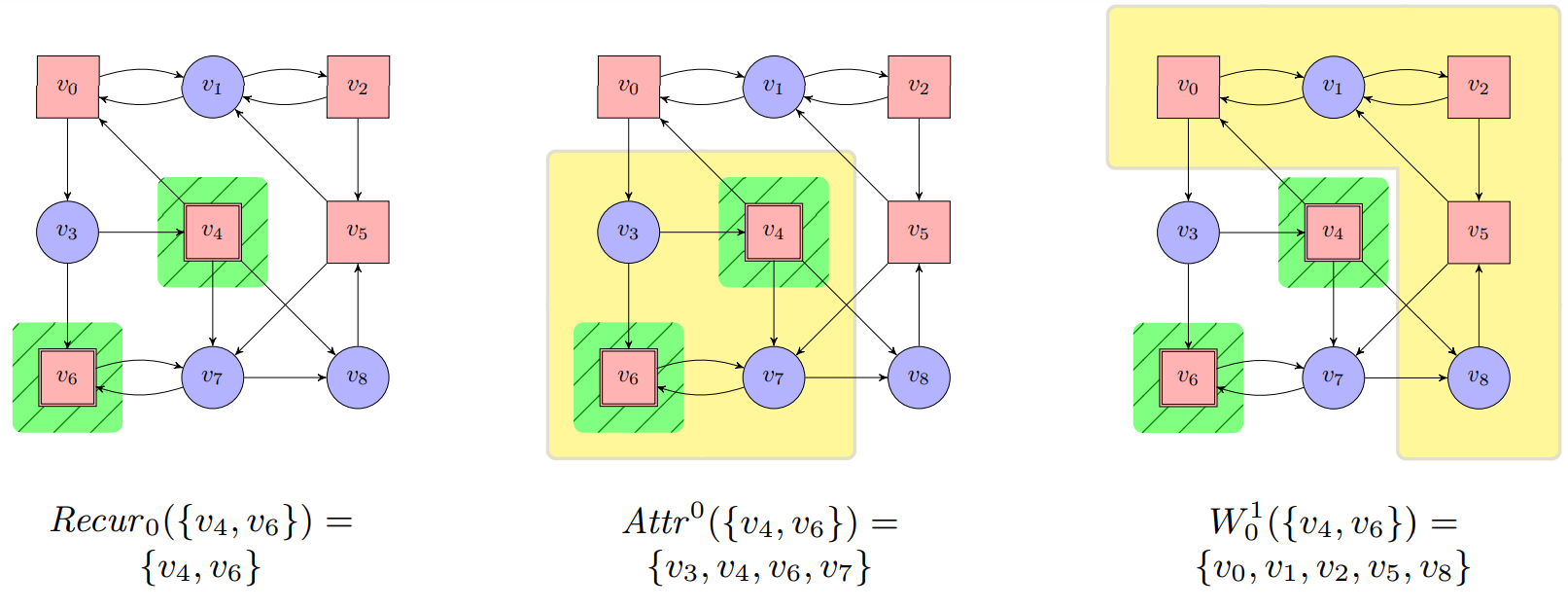
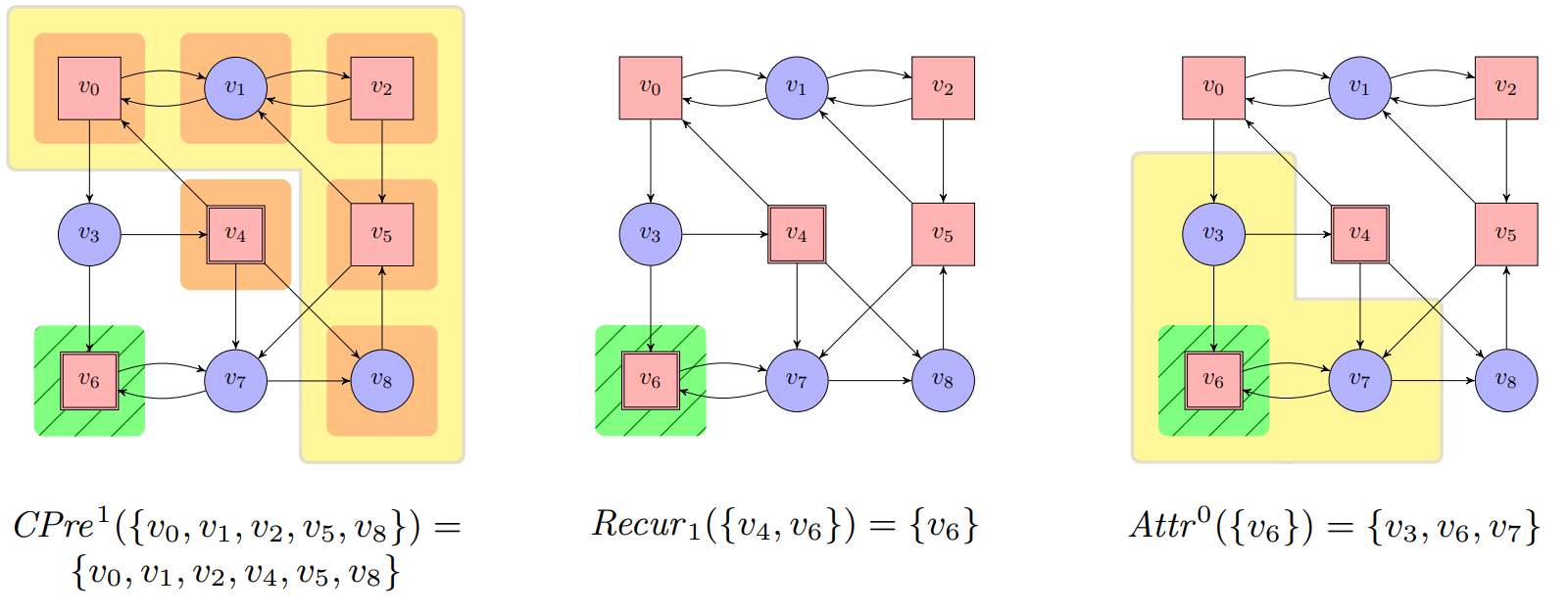
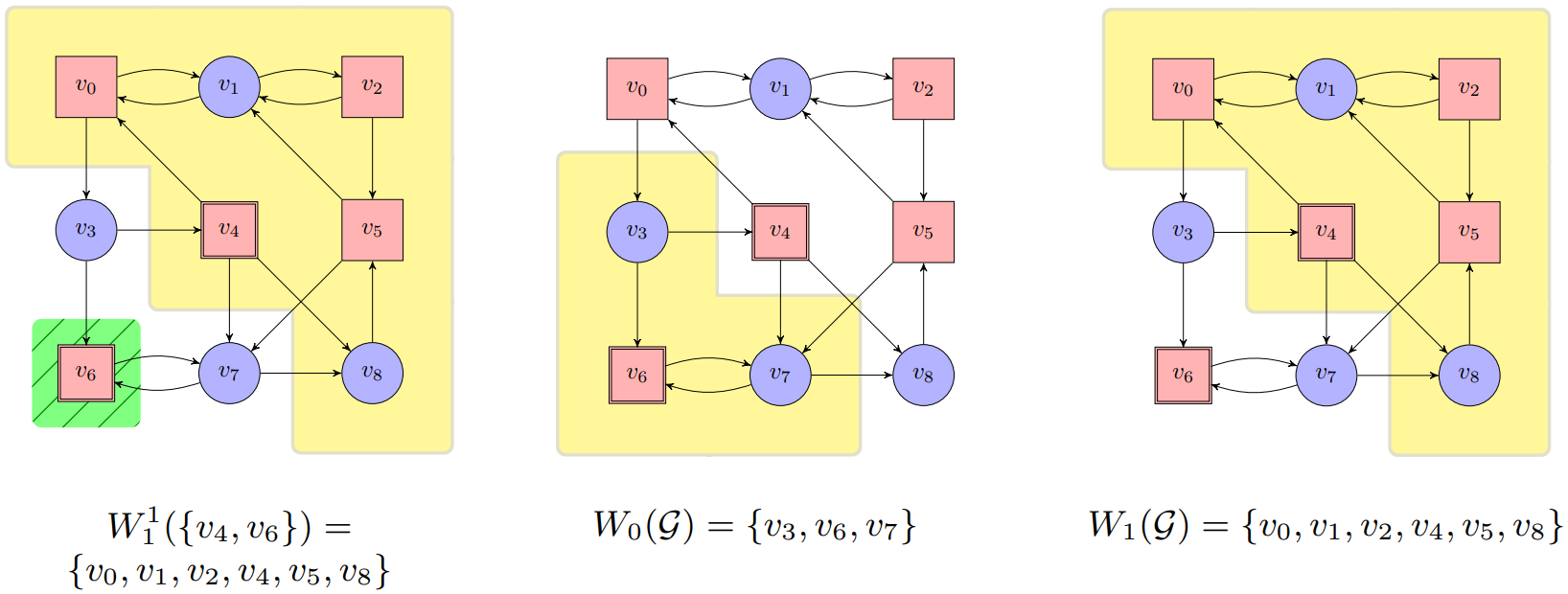
$\textbf{Theorem 11.2. } \textit{Büchi games are memoryless determined. It holds that}\newline W_0(\mathcal{G})=Attr^0(Recur(F)), W_1(\mathcal{G})=V\setminus W_0(\mathcal{G})\textit{. Both players have a uniform winning strategy.}$
Proof
We show for all positions $v\in V$ that
If $v\in Attr^0(Recur(F))$, then $v\in W_0(\mathcal{G})$, with the following uniform memoryless strategy $\sigma$:
We fix some arbitrary total ordering on $V$. For $v\in (Attr^0(Recur(F))\setminus Recur(F))\cap V_0$, we follow the attractor strategy from the proof of Theorem 11.1.
For $v\in Recur(F)\cap V_0$, we choose the smallest $v’\in V$ with $(v,v’)\in E$ and $v’\in Attr^0(Recur(F))$. Such a successor must exist, because otherwise $v\in CPre^{1}(W_n^1(F))$ for some $n\in\mathbb{N}$, and hence $v\notin Recur(F)$.
Every play that is consistent with $\sigma$ visits $Recur(F)\subseteq F$ infinitely often. Hence, $\sigma$ is winning for Player 0.
If $v\in V\setminus Attr^0(Recur (F))$, then $v\in W_1(\mathcal{G})$, with the following uniform memoryless strategy $\tau$:
We again fix an arbitrary total ordering on $V$. We define the memoryless strategies $\tau$ such taht, for $n\in\mathbb{N}$, if a play starts in $v\in W_n^1=V\setminus Attr^0(Recur_n(F))$ and is consistent with $\tau$, there are at most $n$ visits to $F$.
For $n=0$ let $\tau(v)$ be the smallest $v’\in V$ such that $(v,v’)\in E$ and $v’\in V\setminus Attr^0(F)$.
For $n>0$ let $\tau(v)$ be the smallest $v\in W_{n-1}^1(F)$ with $(v,v’)\in E$ if $v\in CPre^1(W_{n-1}^1(F))$ and as the smallest $v’$ in $W_{n}^1(F)$ with $(v,v’)\in E$ otherwise. Such a $v’$ always exists as otherwise $v\in Attr^0(Recur (F))$.
Explaination
Strategy for Player 0
If a position $v$ belongs to $(Attr^0(Recur(F))\setminus Recur(F))\cap V_0$, it must have edges to $Recur(F)$, then choose the smallest $v’$ among those.
If a position $v$ belongs to $Recur(F)\cap V_0$, we need to ensure it will visit $F$ again, so we need to choose an edge that belongs to $Attr^0(Recur(F))$.
Strategy for Player 1
Every position from Player 1 must belong to $W_n^1$, that ensures that only at most n times visits to $F$, otherwise Player 1 has no choice (belongs to $Attr^0(F)$)
For such n = 0, we can ensure it never visit $F$ by choosing smallest $v’$ that does not move to $Attr^0(F)$.
For such n > 0, if it also belongs to $W_{n-1}^1$, then it must have edge(s) that also belongs to $W_{n-1}^1$, otherwise there exist edge(s) belongs to $W_{n}^1$, so that it can stays in winning region of Player 1 without visiting $Attr^0(F)$.
Next chapter: Parity Games
Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com