Previous chapter: Büchi automata (Preliminaries)
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
2.2 Automata over Infinite Words
The operational behavior of an automaton over infinite words is very similar to automaton over finite words:
- Start with an initial state
- Automaton constructs a run by reading one letter of the input alphabet at a time, and
transitioning to a successor state permitted by its transitions.
The major difference between automata over finite and infinite words is the acceptance condition.
$\textbf{Definition 2.1. } \text{ An } \textit{automaton over infinite words } \text{is a tuple }\mathcal{A} = (\Sigma,Q,I,T,Acc)\text{, where}$
$\begin{array}{l}
\hspace{1cm} \cdot \ \Sigma \text{ is a finite } \textit{alphabet} \newline
\hspace{1cm} \cdot \ Q \text{ is a finite set of } \textit{states} \newline
\hspace{1cm} \cdot \ I \subseteq Q \text{ is a subset of } \textit{initial states} \newline
\hspace{1cm} \cdot \ T \subseteq Q \times \Sigma \times Q \text{ is a set of } \textit{transitions} \text{, and} \newline
\hspace{1cm} \cdot \ Acc \subseteq Q^\omega \text{ is the } \textit{accepting condition}
\end{array}$
In the following, we refer an automaton over infinite words simply as an automaton.
Runs of Büchi automata
A run in a Büchi automaton has to transition infinitely many times, and starts with the initial state.
$\textbf{Definition 2.2. }\text{ An }\textit{run }\text{of an automaton }\mathcal{A}\text{ on an infinite input word }\alpha\text{ is an }\newline\text{infinite sequence of states }r=r(0)r(1)r(2)\dots\text{ such that the following hold:}\newline\begin{array}{l}\hspace{1cm} \cdot \ r(0)\in I\newline\hspace{1cm} \cdot \ \text{for all }i\in\mathbb{N},(r(i),\alpha(i),r(i+1))\in T\end{array}$
Example
Below is a graphical representation of an automation over:
- alphabet $\Sigma = \lbrace a,b\rbrace$, and with
- set of states $Q =\lbrace A,B,C,D\rbrace$,
- initial set of states $I =\lbrace A\rbrace$, and
- set of transitions $T =\lbrace (A,a,B),(B,a,C),(C,b,D),(D,b,A)\rbrace$
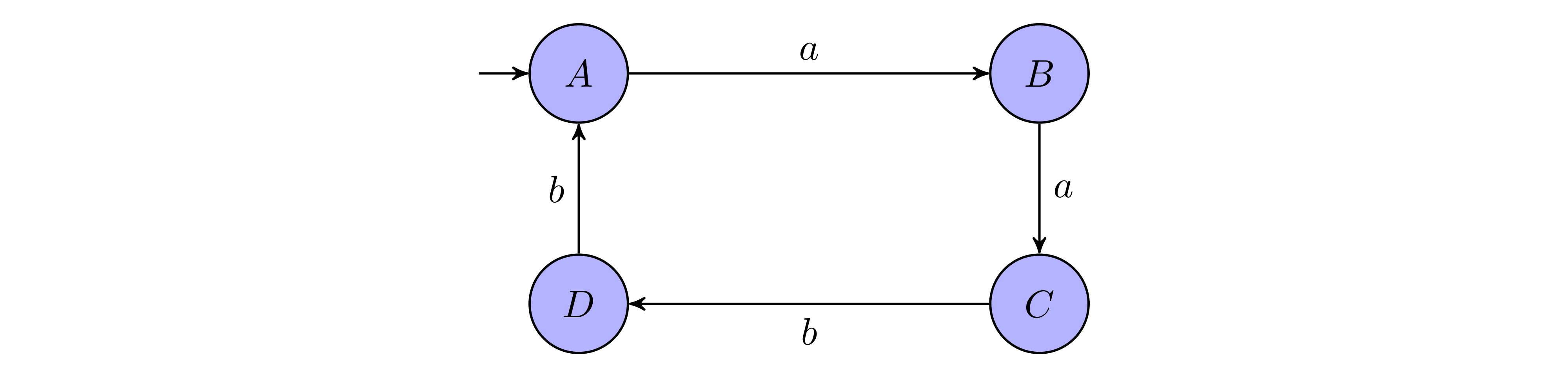
On the infinite input word $aabbaabb\dots$, the (only) run of the automaton is $ABCDABCDABCD\dots$
Deterministic and Complete Automaton
An automaton is deterministic if $|I|\leq 1$ and $\mid\lbrace (q,\sigma,q’)\in T \mid q’\in Q\rbrace|\leq 1$ for every $q\in Q$ and $\sigma\in\Sigma$.
Meaning that the automaton has exactly 1 initial state, and exactly 1 transition from $q$ to $q’$
An automaton is complete if $\mid\lbrace (q,\sigma,q’)\in T \mid q’\in Q\rbrace|\geq 1$ for every $q\in Q$.
Meaning that any two states $(q,q’)$ in the automaton should have at least 1 transitions from $q$ to $q’$.
Therefore, the automaton in the example above is deterministic but not complete.
The transitions of an deterministic and complete automata are usually given as a function $\delta:Q \times\Sigma\rightarrow Q$.
Meaning that the set of all transitions $\delta$ contains any states with any letter.
Accepted Run
$\textbf{Definition 2.3. } \text{ An automaton } \mathcal{A} \textit{ accepts}\text{ an infinite word }\alpha\text{ if: }$
$\begin{array}{l}
\hspace{1cm} \cdot \ \text{there is a run }r\text{ of }\mathcal{A}\text{ on }\alpha\text{, and}\newline
\hspace{1cm} \cdot \ r \text{ is } \textit{accepting}:r\in Acc\end{array}\newline
\text{The } \textit{language recognized }\text{by }\mathcal{A}\text{ is defined as follows: }
\mathcal{L}(\mathcal{A}) = \lbrace \alpha\in\Sigma^\omega\mid\mathcal{A}\text{ accepts }\alpha\rbrace$
We say two automata are equivalent if they have the same language.
Further Reading: Büchi automaton, Omega language
Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com