Previous chapter: Automata over Infinite Words
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
2.3 The Büchi Acceptance Condition
The Büchi Acceptance Condition is given as a set of accepting states $F$.
A run of a Büchi automaton is accepting if some state from this set occurs infinitely often.
Infinite word
For an infinite word $\alpha$ over $\Sigma$, an Infinity Set of $\alpha$ is denoted as:
$$\text{Inf}(\alpha) = \lbrace\sigma\in\Sigma\mid\forall m\in\mathbb{N}.\exists n\in\mathbb{N}.n\geq m \text{ and } \alpha(n)=\sigma\rbrace$$
Meaning that $\text{Inf}(\alpha)$ is a set of all letters $\sigma$ from the alphabet $\Sigma$, so that
for all $m$, you can always find $\sigma$ as the n-th letter of $\alpha$ when there exists an $n$ where $n\geq m$.
This denotes the set of all letters of $\Sigma$ that occur infinitely often in $\alpha$.
Büchi Condition
To express the meaning of “some state from the set of accepting states is reached infinitely often“, we can rewrite our accpeing condition $Acc$ into Büchi Condition $\small\text{BÜCHI} \normalsize (F)$
Here, $\small\text{BÜCHI} \normalsize (F)$ is a set of infinite word that
$\textbf{Definition 2.4. } \text{ The } \textit{Büchi Condition } \small\text{BÜCHI} \normalsize (F)\text{ on a set of states $F\subseteq Q$ is the set}$
$$\small\text{BÜCHI} \normalsize (F) = \lbrace\alpha\in Q^\omega \mid \text{Inf}(\alpha) \cap F \neq \varnothing\rbrace$$ $\text{An automaton }\mathcal{A}=(\Sigma,Q,I,T,Acc)\text{ with }Acc=\small\text{BÜCHI} \normalsize (F)\text{ is called a }\textit{Büchi automaton.}\newline \text{The set $F$ is called the }\textit{set of accepting states.}$
Constrcution of Complete Büchi Automaton
$\textbf{Theorem 2.1. } \textit{For every Büchi Automaton $\mathcal{A}$, there is a complete Büchi Automaton $\mathcal{A}’$} \newline \textit{such that $\mathcal{L}(\mathcal{A}) = \mathcal{L}(\mathcal{A}’)$}$
$\textbf{Example 2.2.}$
Let $\mathcal{A}$ be the automaton from Example 2.1 with Büchi acceptance condition $\small\text{BÜCHI}\normalsize (\lbrace D\rbrace)$. The language of the automaton consists of a single word:
$$\mathcal{L}(\mathcal{A})=\lbrace aabbaabbaabb\dots\rbrace$$
For a Büchi Automaton $\mathcal{A} = (\Sigma,Q,I,T,\small\text{BÜCHI} \normalsize (F))$,
we define the complete Büchi Automaton $\mathcal{A’} = (\Sigma,Q’,I’,T’,\small\text{BÜCHI} \normalsize (F’))$ using:
- $Q’$ = $Q \cup \lbrace q_f\rbrace$ where $q_f$ is a fresh state
- $I’$ = $I$
- $T’$ = $T \cup \lbrace (q,\sigma,q_f) \mid \nexists q’ . (q,\sigma,q’)\in T\rbrace\cup\lbrace (q_f,\sigma,q_f)\mid\sigma\in\Sigma\rbrace$
- $F’$ = $F$
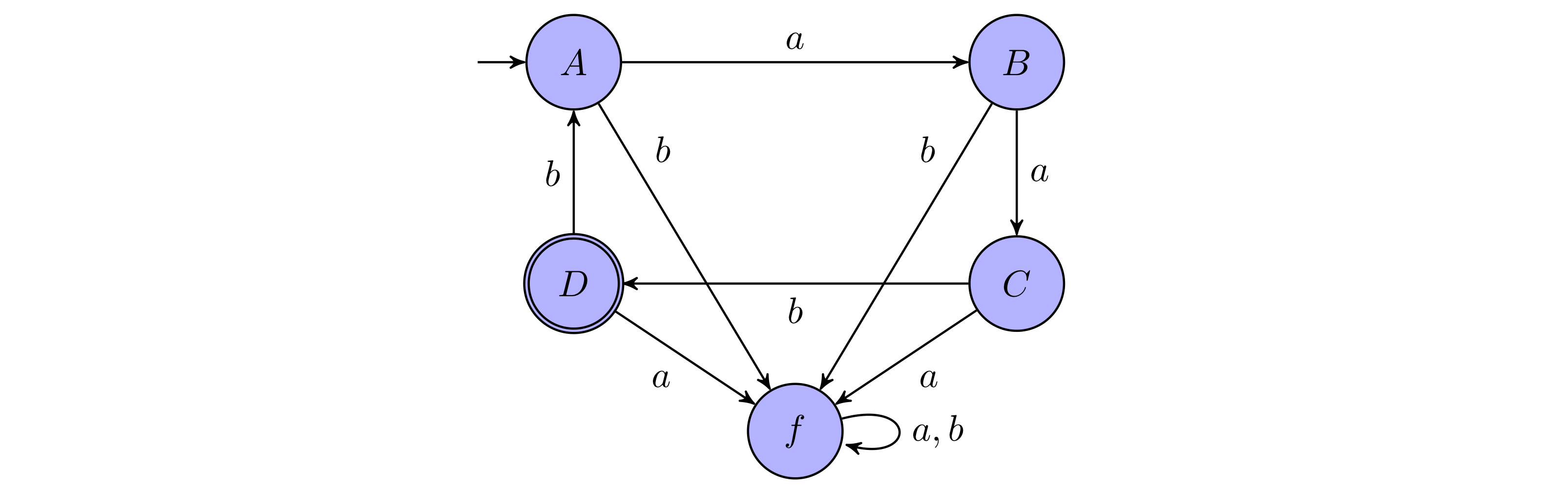
Explaination
First, we add a fresh state $q_f$ the set of state $Q$ without changing the initial and accepting states.
A complete Büchi Automaton requires every states must have transitions for every letters in the alphabet.
So for each states orginally in $Q$, we construct new transitions that the letters are not yet used by the state.
(which is $\nexists q’ . (q,\sigma,q’)\in T$)
Finally, for all transitions from the fresh state are self transitioning, and they include all letters.
(which is $(q_f,\sigma,q_f)\mid\sigma\in\Sigma$)
Formal Proof
The runs of $\mathcal{A’}$ are a superset of those of $\mathcal{A}$.
- During the construction of $\mathcal{A’}$, we have not removed any original transitions, but adding new fresh states.
Furthermore, on any infinite input word, the accepting runs of $\mathcal{A}$ and $\mathcal{A’}$ are the same.
- If $\mathcal{A}$ accepts, $\mathcal{A’}$ also accepts because $\mathcal{A’}$ is a superset.
- If a run reaches new fresh states $q_f$ stays in $q_f$ forever, and
- since $q_f\notin F’$, such a run is not accepting.
Summary
A complete deterministic automaton may be viewed as a total function from $\Sigma^\omega$ to $Q^\omega$.
A complete (possibly nondeterministic) automaton produces at least one run for every input word.
Next chapter: Kleene’s Theorem
Further Reading: Büchi automaton, Omega language
Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com