AGV 4.2 -- Complementation of deterministic Büchi Automata

Notes > UdS AGV

Created At : 2024-11-19 23:12

Count:1k Views :

Introduction

Previous chapter: Deterministic vs. Nondeterministic Büchi Automata

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

For regular languages, Complementation is very simple: one translates a given complete deterministic automaton $\mathcal{A}$ that recognizes some language $L\subseteq\Sigma^*$ into an automaton $\mathcal{A’}$ that recognizes the complement $\Sigma^*\setminus L$ by complementing the set of final states, i.e., $F’=Q\setminus F$.

For deterministic Büchi automata, the construction is tricky, because it introduces nondeterminism

$\textbf{Construction 4.1. }\text{Let }\mathcal{A}=(\Sigma,Q,I,T,\small\text{BÜCHI} \normalsize (F))\text{ be a complete deterministic Büchi}\newline\text{automaton, where we assume w.l.o.g. that } Q\neq\varnothing. \text{ We construct a Büchi automaton}\newline\mathcal{A’}=(\Sigma,Q’,I’,T’,\small\text{BÜCHI} \normalsize (F’))\text{ with }\mathcal{L}(\mathcal{A’})=\Sigma^\omega\setminus\mathcal{L}(\mathcal{A})\text{ as follows:}$
$\begin{array}{lrll}
\hspace{1cm} \cdot &Q’&=&(Q\times\lbrace 0\rbrace)\cup((Q\setminus F)\times\lbrace 1\rbrace)\newline
\hspace{1cm} \cdot &I’&=&I\times\lbrace 0\rbrace\newline
\hspace{1cm} \cdot &T’&=&\lbrace ((q,0),\sigma,(q’,i))\mid(q,\sigma,q’)\in T,i\in\lbrace 0,1\rbrace,(q’,i)\in Q’\rbrace \cup \newline
\hspace{1cm} \ &&&\lbrace ((q,1),\sigma,(q’,1))\mid(q,\sigma,q’)\in T,q’,q’\in Q\setminus F\rbrace\newline
\hspace{1cm} \cdot &F’&=&(Q\setminus F)\times\lbrace 1\rbrace
\end{array}$

	Explaination
$Q’$	Uses two copies of the given automaton $\mathcal{A}$, mark them seperately using $\lbrace 0\rbrace$ and $\lbrace 1\rbrace$, notice that all accpeting states from $\lbrace 1\rbrace$ are eliminated
$I’$	The complemented automaton starts from initial states from $\lbrace 0\rbrace$.
$T’$	The switch from $\lbrace 0\rbrace$ and $\lbrace 1\rbrace$ happens nondeterministically. And once you enter the second copy $\lbrace 1\rbrace$, it stays forever.
$F’$	The automaton $\mathcal{A’}$ accepts if the run ends up in the second copy, which means that, on the unique run of $\mathcal{A}$ on the input word, the accepting states of $\mathcal{A}$ are only visited finitely often.

Note that the resulting automaton is nondeterministic. This is, in general, unavoidable.

This is because there are languages, such as $L=(b^*a)^\omega$ where the language itself is recognizable by a deterministic Buchi automaton, while its complement $\Sigma^\omega\setminus L$ can only be recognized by a nondeterministic Büchi automaton.

$\textbf{Theorem 4.3. }\textit{For every deterministic Büchi automaton }\mathcal{A}\textit{, there exists a Büchi automaton }\mathcal{A’}\newline\textit{ such that }\mathcal{L}(\mathcal{A’})=\Sigma^\omega \setminus\mathcal{L}(\mathcal{A}).$

Explained in Human Language

$\mathcal{L}(\mathcal{A’})\subseteq\Sigma^\omega \setminus\mathcal{L}(\mathcal{A}):$

To prove that “If $\alpha$ is accepted by $\mathcal{L}(\mathcal{A’})$, then it is also accepted by the complement of $\mathcal{L}(\mathcal{A})$”, we can show that every state in $\mathcal{A’}$ is same as $\mathcal{A}$, but as long as it switched to $\lbrace 1\rbrace$, it stays forever and there is no accepting states of $\mathcal{A}$.

Therefore, every accepted word in $\mathcal{L}(\mathcal{A’})$ is also accepted in $\Sigma^\omega \setminus\mathcal{L}(\mathcal{A})$.

$\mathcal{L}(\mathcal{A’})\supseteq\Sigma^\omega \setminus\mathcal{L}(\mathcal{A}):$

To prove that “If $\alpha$ is accepted by the complement of $\mathcal{L}(\mathcal{A})$, then it is also accepted by $\mathcal{L}(\mathcal{A’})$”, we assume there’s a word $\alpha$ that is not accepted by $\mathcal{L}(\mathcal{A})$.

Since $\mathcal{A}$ is complete and deterministic, so the run on $\alpha$ is still infinite, yet never visit the accepted states infinitely often. i.e. starting from certain position, it will never visit the accepting states anymore.

We can treat that position as the switch from $\lbrace 0\rbrace$ and $\lbrace 1\rbrace$ in $\mathcal{A’}$ occurs. And therefore $\alpha$ is an accepted word in $\mathcal{L}(\mathcal{A’})$.

Formal Proof

Let $\mathcal{A’}$ be constructed from the given deterministic Büchi automaton $\mathcal{A}$ (which we
assume, w.l.o.g., to be complete) by Construction 4.1. We prove that $\mathcal{L}(\mathcal{A’})=\Sigma^\omega \setminus\mathcal{L}(\mathcal{A}).$

$\mathcal{L}(\mathcal{A’})\subseteq\Sigma^\omega \setminus\mathcal{L}(\mathcal{A}):$

For every word $\alpha\in\mathcal{L}(\mathcal{A’})$ we have an accepting run: $r’:(q_0,0)(q_1,0)\dots(q_j,0)(q’_0,1)(q_1,1)\dots$ on $\mathcal{A}$. Hence, $r:q_0q_1\dots q_jq_0’q_1’\dots$ is the unique run of $\mathcal{A}$ on $\alpha$. Since $q_0’,q_1’,\dots\in Q\setminus F$, we have that $\text{Inf}(r)\subseteq Q\setminus F$. Hence, $r$ is not accepting and $\alpha\in\Sigma^\omega\setminus\mathcal{L}(\mathcal{A})$.

$\mathcal{L}(\mathcal{A’})\supseteq\Sigma^\omega \setminus\mathcal{L}(\mathcal{A}):$

Let $\alpha\notin\mathcal{L}(\mathcal{A’})$ be some word that is not in the language of $\mathcal{A}$. Since $\mathcal{A}$ is complete and deterministic, there exists a unique run $r:q_0q_1q_2\dots$ of $\mathcal{A}$ on $\alpha$ and $\text{Inf}(r)\cap F=\varnothing$. Thus, there exists a $k\in\mathbb{N}$ such that $q_j\notin F$ for all $j > k$.

This gives us the run: $r’:(q_0,0)(q_1,0)\dots(q_j,0)(q’_0,1)(q_1,1)\dots$ of $\mathcal{A’}$ on $\alpha$ with $\text{Inf}(r)\subseteq ((Q\setminus F)\times\lbrace 1\rbrace)=F’$. Hence, $r’$ is accepting and therefore $\alpha\in\mathcal{L}(\mathcal{A’})$.

Example: $\mathcal{L}(\mathcal{A})=(b^\ast a)^\omega$ and $\mathcal{L}(\mathcal{A’})=(a+b)^\ast b^\omega$

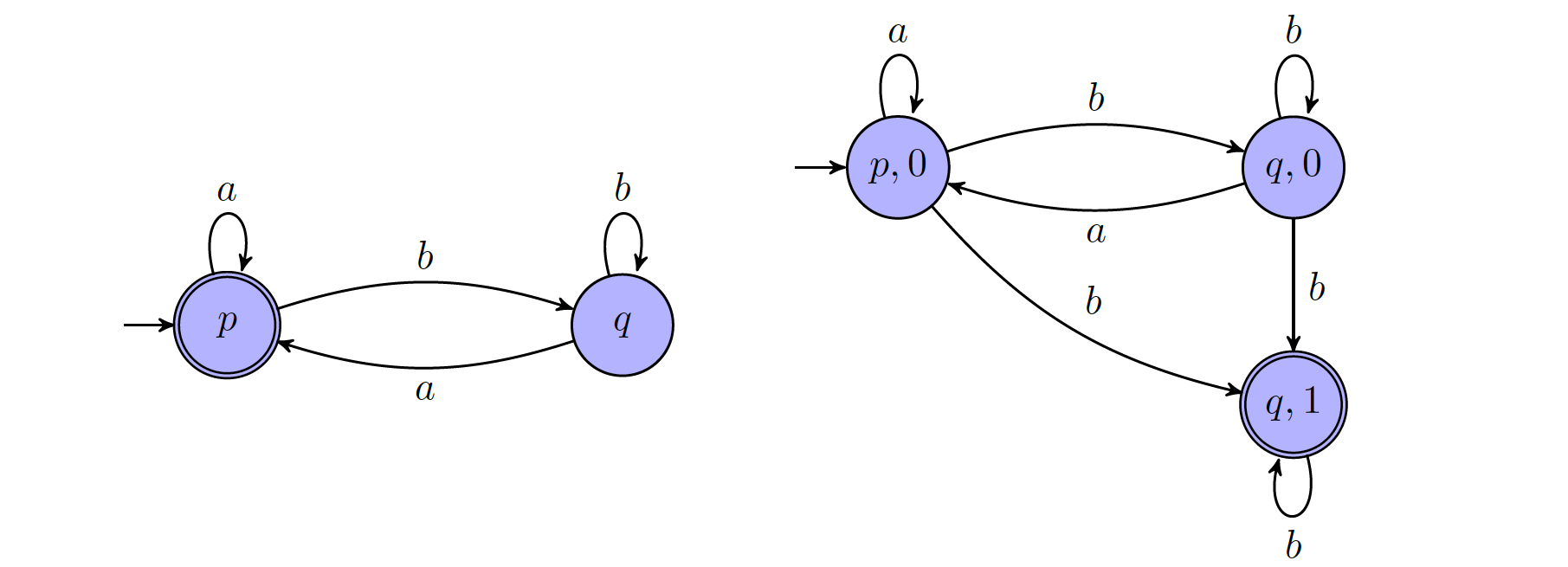
Note that, since not all $\omega$-regular languages can be recognized by deterministic Büchi automata, Construction 4.1 does not provide us with a complementation construction for all $\omega$-regular languages. Such a general construction is the subject of the following section.

Next chapter: Infinite Directed Acyclic Graph (DAG)