Automata, Games, and Verification (Portal)

Previous chapter: Complementation of deterministic Büchi Automata

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Reasoning about all runs of an automaton

Since complementation inevitably introduce nondeterminism, we need to check whether all runs of the automaton on the word are rejecting to determine whether a word is in the complement of the language recognized by this Büchi automaton.

Example

Consider the following nondeterministic Büchi automaton $\mathcal{A}$. Its language consists of all infinite words over $\lbrace a,b\rbrace$ with infinitely many bs, i.e., $(a^*b)^\omega$:

$\textbf{Definition 5.1. }\text{Let }\mathcal{A}=(\Sigma,Q,I,T,\small\text{BÜCHI} \normalsize (F))\text{ be a Büchi automaton. The run DAG of }\mathcal{A}\newline\text{on a word }\alpha\in\Sigma^\omega\text{ is the directed acylic graph }G=(V,E)\text{, where}$
$\begin{array}{lll}
\hspace{1cm} \cdot \ V&=&\cup_{i\geq0}(Q_i\times\lbrace i\rbrace)\text{ with }Q_0=I\text{ and}\newline
\hspace{1.1cm} \ Q_{i+1}&=&\lbrace q’\mid(q,\alpha(i),q’)\in T\text{ for some }q\in Q\rbrace\newline
\hspace{1cm} \cdot \ E&=&\lbrace((q,i),(q’,i+1))\mid i\geq 0,(q,\alpha(i),q’)\in T\rbrace.\end{array}$
$\text{For a natural number }i\text{, we refer to the set }Q_i\text{ as the }\textit{level }i\text{ of the DAG.}$

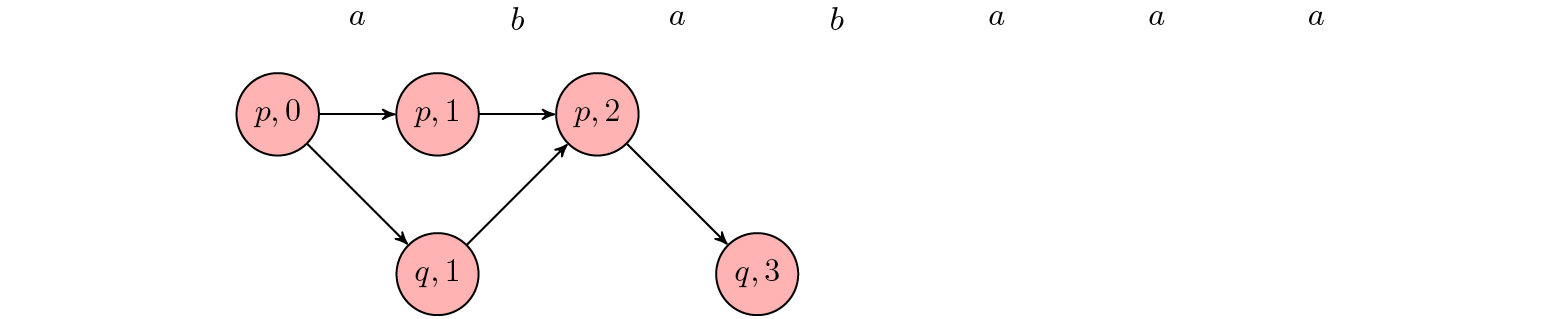
Using infinite directed acyclic graph (DAG) to represent the set of all runs on a particular word, e.g., $ababa^\omega$.

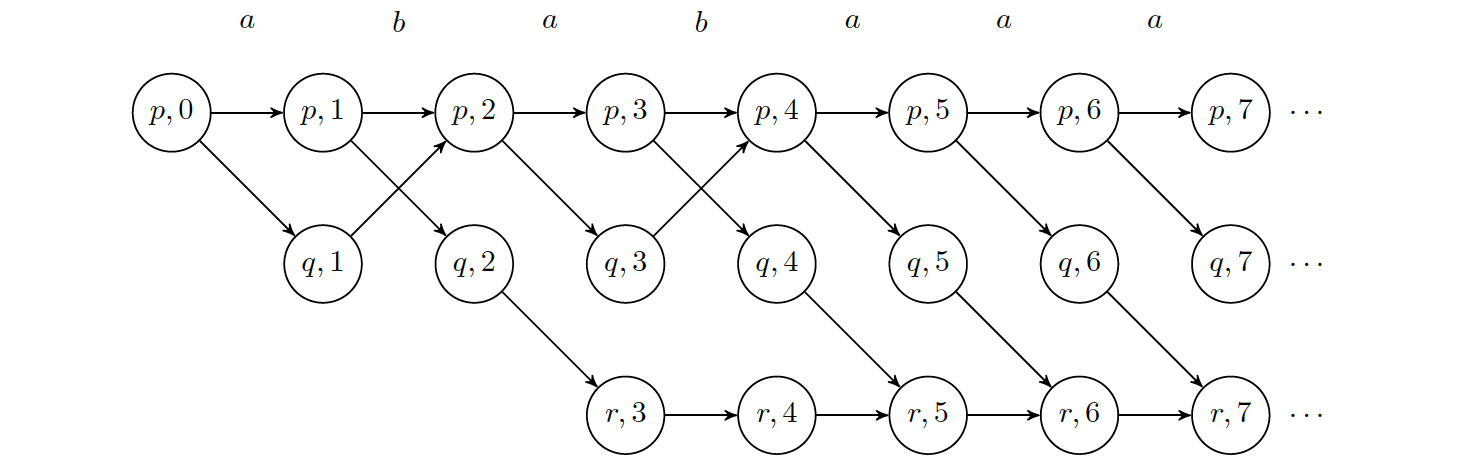
In the above example: the word $\alpha=ababa^\omega$ has only two b‘s and hence must be rejected by $\mathcal{A}$.

Since the automaton is nondeterministic, a single word of $\mathcal{A}$ will have multiple runs on $\alpha$, represented by each path in DAG. The path is called accepting if and only if its corresponding run is accepting, i.e., the path visits $F\times\mathcal{A}$ infinitely often.

Graph Pruning

To show the non-acceptance of $\alpha$ by $\mathcal{A}$, we can systematically identifying and pruning away vertices of the run DAG that only lead to rejecting paths until the graph is empty using the following definitions:

Vertices in DAG	Defintiion
Endangered	when they only have finitely many descendants
Safe	when they are not in $F\times\mathcal{A}$, and none of its descendants are in $F\times\mathcal{A}$ either

We start with a graph $G_0=G$. Each iteration $j\geq 0$ of our pruning will consist of two steps:

1. in step $2j$, the graph = $G_{2j}$, remove all endangered vertices, graph after removal = $G_{2j+1}$
2. in step $2j+1$, the graph = $G_{2j+1}$, remove all safe vertices, graph after removal = $G_{2j+2}$

Step 0: Remove endangered vertices

• Input: $G_0$ ↑ (using example above), Output: $G_1$ ↓

Since there’s no endangered verticies, $G_0$ = $G_1$

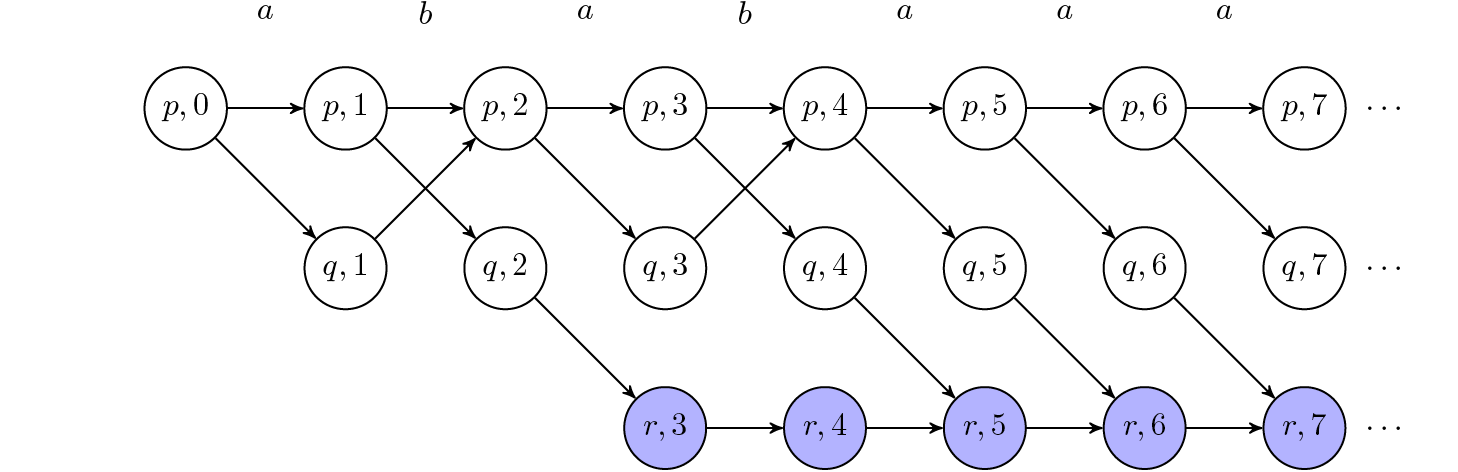
Step 1: Remove safe vertices (marked as blue)

• Input: $G_1$ ↑, Output: $G_2$ ↓

As we can see all vertices that in state r stay in r forever (accepting state is q). Therefore those path can never be accepted and they are safe.

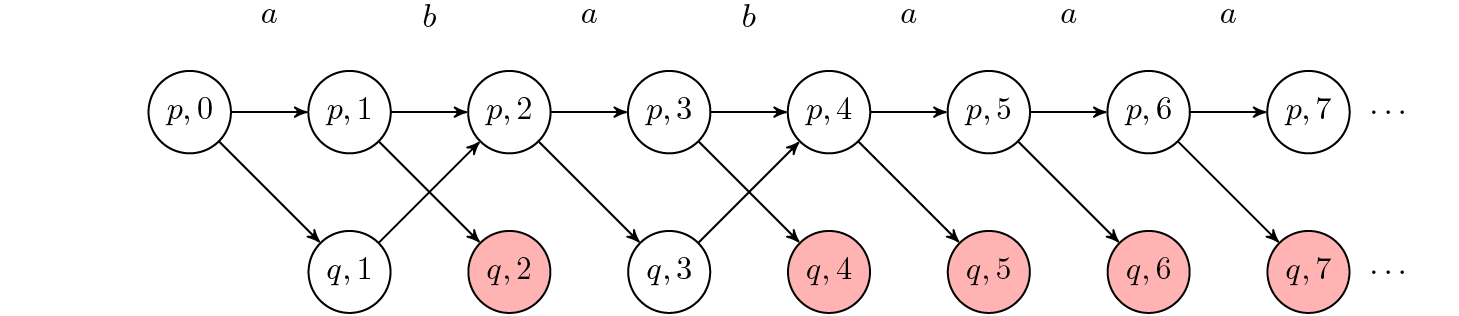
Step 2: Remove endangered vertices (marked as red)

• Input: $G_2$ ↑, Output: $G_3$ ↓

After safe verticies in r are removed, paths towards r from q become dead end. Therefore they are now endangered.

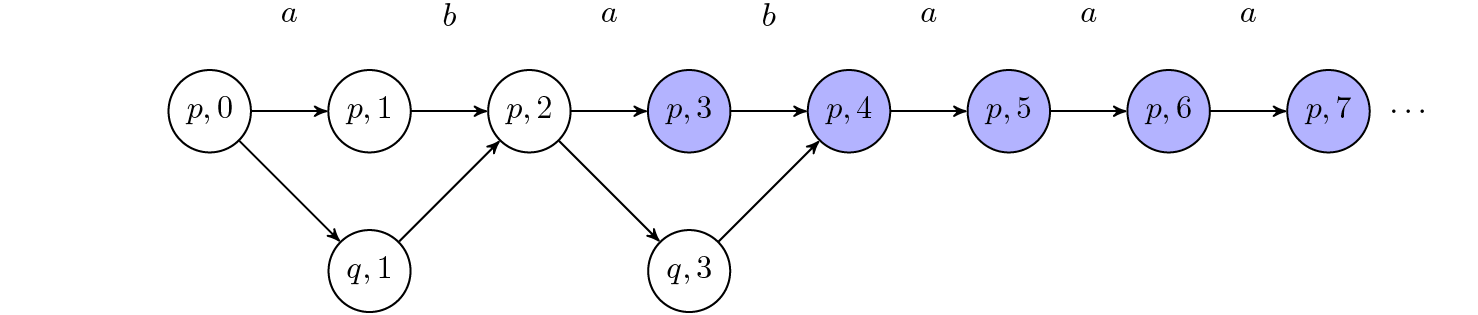
Step 3: Remove safe vertices (marked as blue)

• Input: $G_3$ ↑, Output: $G_4$ ↓

Now all the vertices starting from (p,3) stay in p forever. Therefore they are safe as well.

Step 4: Remove endangered vertices (marked as red)

• Input: $G_4$ ↑, Output: $G_5$ ↓

Now the graph is finite, meaning all the vertices in the graph are endangered.

Therefore, graph $G_5$ will be an empty graph, which means there’s no accepting path and thus the word $ababa^\omega$ is rejected.

Explaination

We start from removing endangered verticies in step 0 because they can never infinitely reach the accepting states. Then we can remove all Safe verticies in step 1 because they never visit accepting states anymore.

For the subsequent pruning, if a vertex v of the original run DAG is pruned away in step $2j$ because it is endangered in $G_{2j}$, it means that all paths from v in the original run DAG can reach were pruned away in the earlier steps.

Similarly, if a vertex v of the original run DAG is pruned away in step $2j+1$ because it is safe in $G_{2j+1}$, it means that v corresponds to a non-accepting state. And furthermore, all paths from v in the original run DAG either avoid accepting vertices, or eventually reach a vertex that was pruned away in the earlier steps.

So we can see that if a vertex is pruned away, all paths from that vertex are rejecting. Hence, if our scheme eventually obtains the empty graph, the pruning is a proof of the non-acceptance of the word by the automaton.

We formalize this type of reasoning as a ranking, which labels the vertices with numbers. We will define ranking in the next chapter.

---

Next chapter: Ranking of DAG

Further Reading:

---

Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com