AGV 5.2 -- Ranking of DAG

Notes > UdS AGV

Created At : 2024-11-21 01:19

Count:1.3k Views :

Ranking
From Ranking to Rank
From Rank to Odd Ranking
Conclusion

Previous chapter: Infinite Directed Acyclic Graph (DAG)

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Ranking

last section, we have introduced the DAG and the pruning method to reason about the run of the word on a non-deterministic Büchi automaton. We know that pruning can be use to prove the non-acceptance of the word by automaton is we obtains an empty graph eventually.

In this section, we will introduce ranking, which can formalize our pruning construction.

$\textbf{Definition 5.2. }\text{(Ranking). A }\textit{ranking}\text{ on a run DAG } G=(V,E)\text{ is a function }f:V\rightarrow\newline\lbrace 0,\dots,2|Q|\rbrace\text{ such that:}$
$\begin{array}{l}\hspace{1cm} 1. \ \text{ If }q\in F\text{, then }f((q,i))\text{ is even for all }i.\newline\hspace{1cm} 2. \ \text{ If }(v,v’)\in E\text{, we have that }f(v’)\leq f(v).\end{array}\newline$
$\text{A ranking } f\text{ is }\textit{odd}\text{ if, for each even }j\text{, there is no infinite path in }G\text{ that consists only }\newline\text{of verticies }v\text{ such that }f(v)=j.$

By the above definition, we can see:

All verticies that contains state q (the accepting state) are marked as even rank.
Verticies will never have lower rank than their successors.

Most importantly, it introduced a new concept: Odd Ranking. Meaning that the run of the DAG is rejected.

From Ranking to Rank

Now, let’s consider the function $rank:V\rightarrow\lbrace 0,\dots,2|Q|\rbrace$, where

$rank(q,i)=2j$ iff $(q,i)$ is endangered in $G_{2j}$, and
$rank(q,i)=2j+1$ iff $(q,i)$ is safe in $G_{2j+1}$.

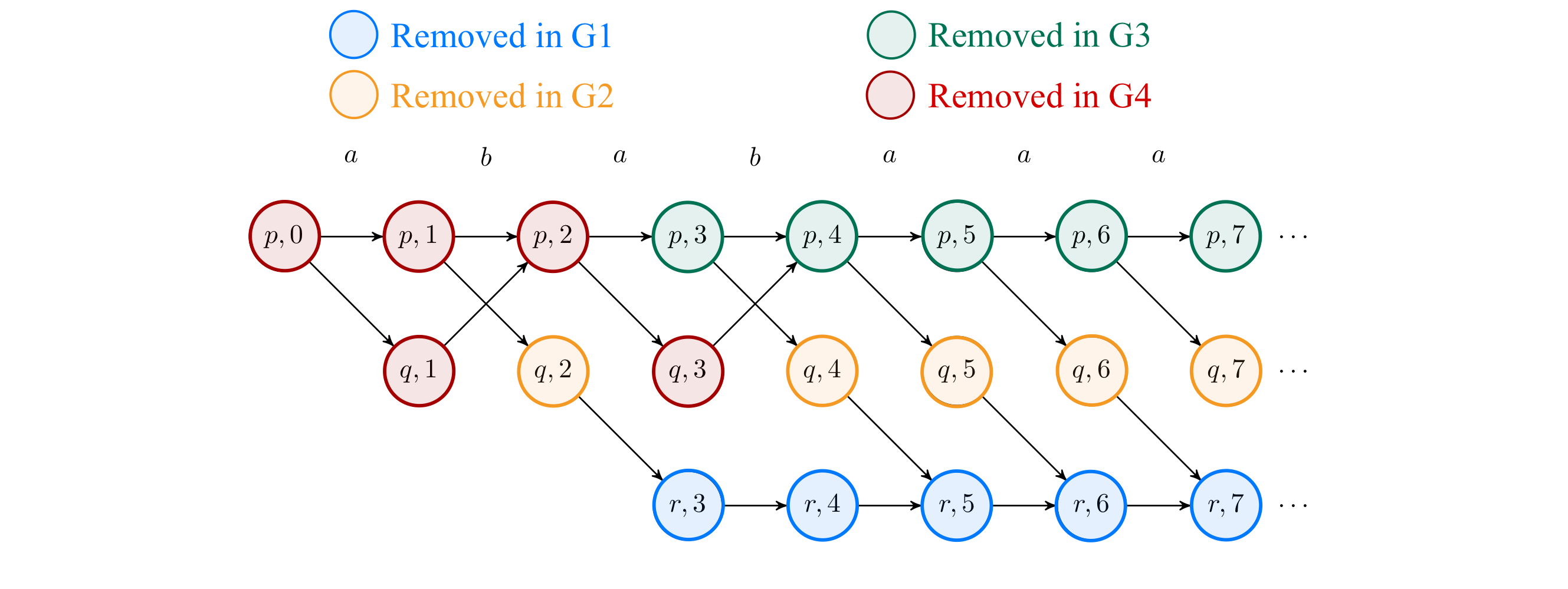
By tracking our pruning procedure, we can easily identify their rank now.
Blue verticies that remove in $G_1$ are safe, thus their rank are 1, and so as orange (2), green (3) and red (4).

From Rank to Odd Ranking

Now back to odd ranking, by our new function $rank$, we can prove the following lemma.

$\textbf{Lemma 5.1. }\newline\textit{A Büchi automaton }\mathcal{A}\textit{ reject the word }\alpha\textit{ iff the run DAG of }\mathcal{A}\textit{ on }\alpha\textit{ has an odd ranking}$

Proof

If the run DAG of $\mathcal{A}$ on $\alpha$ has an odd ranking, then $\alpha$ is rejected

By the definition above, we know that graph with odd ranking has no infinite path that settles on only even rank $f(v)=j$. Which means:

every run of $\mathcal{A}$ on $\alpha$ gets stuck, or,
eventually settles on vertices with a constant odd rank, since ranks are not increasing.

In which case the run eventually only visits states that are not accepting.

If $\alpha$ is rejected, then the run DAG of $\mathcal{A}$ on $\alpha$ has an odd ranking

Since we know pruning leads to rejecting with function $rank$. Therefore, instead of using odd ranking directly, we try to show the function $rank$ is the odd ranking. To prove this, we need to show that:

All vertices are indeed pruned away, latest by step $2|Q|$.
Accepting vertices must have an even rank
The rank cannot increase upon traversing an edge.
There is no infinite path that consists only of vertices of even rank.

Requirement 1: All vertices are indeed pruned away, latest by step $2|Q|$

Here, we define the width of a level $j$ in a graph $G_i$ as the number of vertices of the form $(q,j)$ in $G_i$.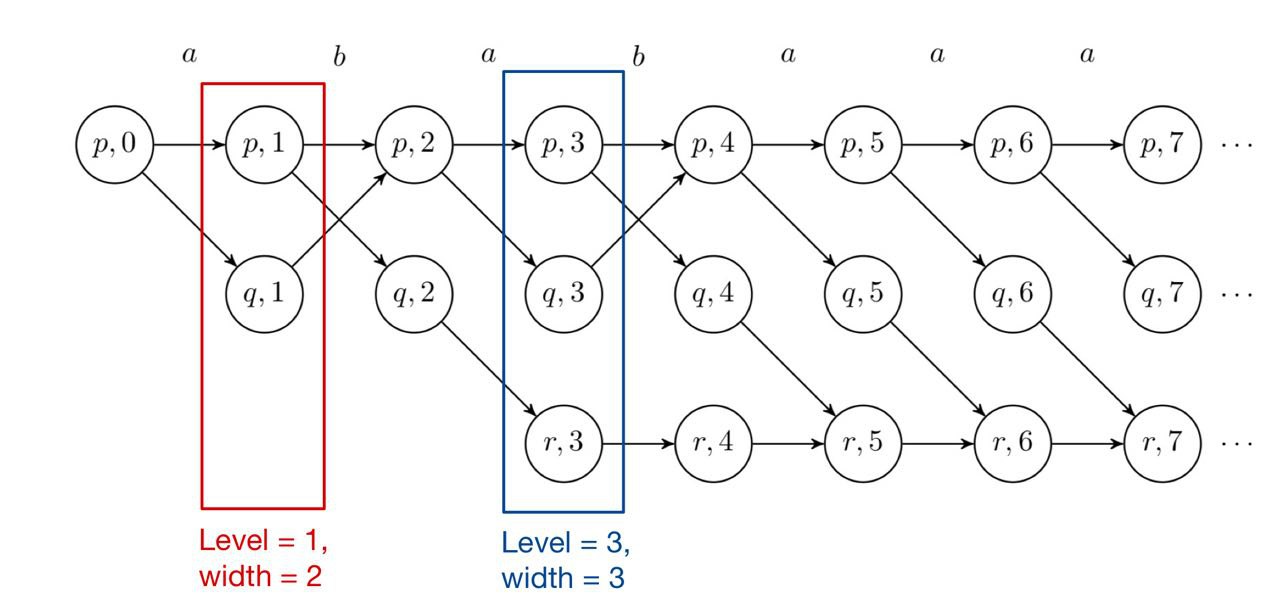

Assume we are in step $2j$, it removes all endangered vertices from $G_{2j}$. Then how would $G_{2j+1}$ become?

become empty (all vertices in $G_{2j}$ are endangered)
still has infinitely many vertices
(by definition, vertices that not endangered always have some infinite path, also because $\infty-n=\infty$)

In scenario 2, since our premise is that the word is rejected, there must exist a safe vertex in $G_{2j+1}$. If there’s no safe vertex, then those vertices are either accepting, or has a path to accepting vertex, which contradicts to our premise.

a) Each iteration there must be at least one safe vertex being removed

Among all the safe vertices in $G_{2j+1}$, consider the vertex $(q,m)$ which has the smallest $m$ (closest to the beginning). All descendants of this vertex in $G_{2j+1}$ are also safe (because safe refers to the whole path).

Therefore, these safe vertices will be pruned away in step $2j+1$. Observe the affect towards the width after these deletions:

At the beginning of iteration $0$, each level has width at most $|Q|$ (max. no. of states).
In every iteration $j$, the widths of all levels $i\geq m$ decrease by at least 1.
(because vertex $(q,m)$ and all its descendants in $i\geq m$ are removed)

b) If one safe vertex is removed, all its descendants will also be removed

By a) and b), we can ensure that after $|Q|$ iterations of safe vertices removal there must be some level $m$ contains no more vertices, which means now the graph terminate in $m$ and it is a finite graph.

By including the iteration of endangered vertices, we can conclude that in step $2|Q|$, $G_{2|Q|}$ must be a finite graph, all vertices are endangered, thus it will prune all vertices away.

Requirement 2: Accepting vertices must have an even rank

Since accepting vertices are not safe, and our premise it that the word is rejected. That means the path contains accepting verticeis can only be finite, which means they are always endangered.

In our rank function, endangered vertices have even rank and thus accepting vertices always have even rank.

Requirement 3: The rank cannot increase upon traversing an edge

Suppose there is a $(q’,i+1)$ that is pruned later than $(q,i)$. Consider the step $j$ at which $(q,i)$ is pruned. The graph $G_j$ would have contained both vertices, along with their edge.

If $j$ is even, it means that $(q,i)$ has even rank, and endangered in $G_j$ , and hence so must be its successor $(q’,i+1)$, meaning that it is pruned at step $j$.

If $j$ is odd, then $(q,i)$ was established to be safe in Gj , implying the safety of its successor too. In both cases, the pruning of $(q’,i+1)$ in the same step is inevitable.

Requirement 4: There is no infinite path of only even-ranked vertices

If such a path exists, since ranks do not increase along a path, and there are only finitely many ranks, this path will eventually consist only of vertices of rank $2j$.

However, only endangered verticies will have even rank in $G_{2j}$, and endangered vertices only have finite paths.

Conclusion

With the above properties and proofs, we know that:

the run DAG of $\mathcal{A}$ on $\alpha$ has an odd ranking = $\alpha$ is rejected
Pruning method with $rank$ function = odd ranking

So if a word is rejected, its run DAG always becomes an empty graph after pruning, and if a run DAG eventually becomes an empty graph after pruning, it must be rejected by $\mathcal{A}$.

With these definition, we can now construct complementation of Büchi automaton $\mathcal{A}$ using the run DAG of $\mathcal{A}$ and the odd ranking. Let see how is it done in the next section.

Next chapter: Complement Büchi Automaton with Odd Ranking