Previous chapter: Expressing Program Properties using LTL
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Semantics
An LTL formula $\varphi$ over $AP$ defines the following language over the alphabet $2^{AP}$:
$\hspace{1cm} \mathcal{L}(\varphi)=\lbrace\alpha\in(2^{AP})^\omega\mid\alpha\models\varphi\rbrace$
where $\models$ is the smallest relation satisfying:
$\begin{array}{lllll}
\hspace{1cm} \alpha & \models & p & \text{iff} & p\in\alpha(0) \ \ \ \ (\text{i.e., }\alpha(0)\models p)\newline
\hspace{1cm} \alpha & \models & \varphi_1\wedge\varphi_2 & \text{iff} & \alpha\models\varphi_1\ \text{ and }\ \alpha\models\varphi_1\newline
\hspace{1cm} \alpha & \models & \neg\varphi & \text{iff} & \alpha\not\models\varphi\newline
\hspace{1cm} \alpha & \models & \bigcirc\varphi & \text{iff} & \alpha[1,\infty]=\alpha(1)\alpha(2)\alpha(3)\dots\models\varphi\newline
\hspace{1cm} \alpha & \models & \varphi_1\ \mathcal{U}\ \varphi_2 & \text{iff} & \exists j\geq0.\ \alpha[j,\infty]\models\varphi_2\ \text{ and }\ \alpha[i,\infty]\models\varphi_1\text{ for all }0\leq i\leq j\newline
\end{array}$
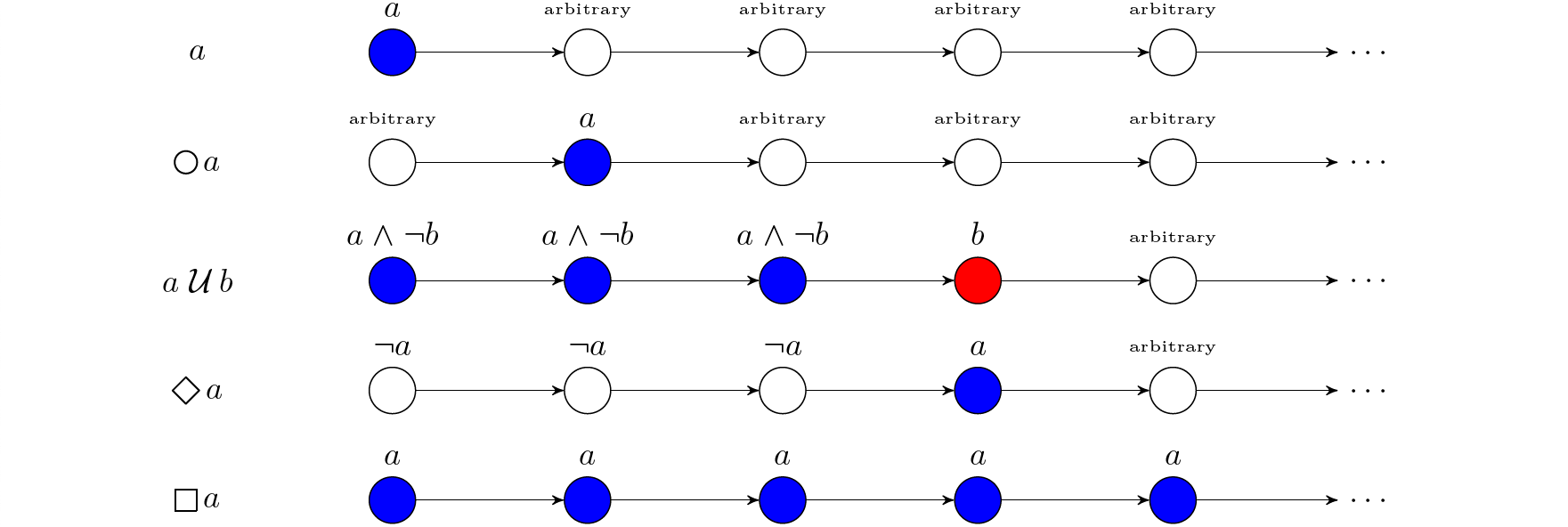
For the temporal operators, the semantics can be visualized as below:
From LTL to $\omega$-regular languages
All LTL-definable properties are $\omega$-regular, but NOT ALL $\omega$-regular languages can be defined in LTL.
Why can’t we? What is the limitation of LTL formula?
Counting and Non-counting Languages
Let say we want to express:
An arbitrary even sequence of $\varnothing$ symbols, followed by an infinite sequence of $p$ symbols
In $\omega$-language it is $(\varnothing\varnothing)^\ast\lbrace p\rbrace^\omega$. However, this cannot be defined in LTL, because it is a counting language.
$\textbf{Definition 6.1. }\text{A Language }L\subseteq\Sigma^\omega\text{ is }\textit{non-counting}\text{ iff}$
$$\exists n_0\in\mathbb{N}.\ \forall n\geq n_0.\ \forall v,w\in\Sigma^\ast, \alpha\in\Sigma^\omega.\ vw^n\alpha\in L\Leftrightarrow vw^{n+1}\alpha\in L$$
For some threshold $n_0$, and a word with prefix $w$ which repeated $n$ times and $n\geq n_0$. For every $n$ we picked, if we can always find a pair of words $vw^{n}\alpha,vw^{n+1}$ that are both accepted by language $L$, then $L$ is non-counting.
For example, in $L_1=(\varnothing\varnothing)^\ast\lbrace p\rbrace^\omega$, if $(\varnothing)^n\lbrace p\rbrace^\omega\in L_1$, then $(\varnothing)^{n+1}\lbrace p\rbrace^\omega\not\in L_1$, so $L_1$ is counting with $n_0=1$.
$\textbf{Theorem 6.1. }\textit{ For every LTL-formula }\varphi,\mathcal{L}(\varphi)\textit{ is non-counting.}$
Proof
We prove the theorem by structural induction on $\varphi$, going through its sematics:
$\textbf{Case }\varphi=p:$
$\hspace{1cm}$ Simply choose the length $n_0=1$, (because $\alpha\models p\text{ iff }p\in\alpha(0)$)
$\textbf{Case }\varphi=\varphi_1\wedge\varphi_2:$
$\hspace{1cm}$ By induction hypothesis, If $\varphi_1$ and $\varphi_2$ are non-counting, then $\mathcal{L}(\varphi_1)$ and $\mathcal{L}(\varphi_2)$ have threshold $n_0’$ and
$\hspace{1cm}$ $n’’_0\in\mathbb{N}$ respectively. We can choose $n_0=\text{max}\lbrace n’_0,n’’_0\rbrace$ to ensure $\varphi$ is also non-counting. (max. because
$\hspace{1cm}$ the larger the $n_0$, less $n$ is required to be non-counting)
$\textbf{Case }\varphi=\neg\varphi_1:$
$\hspace{1cm}$ If $\varphi_1$ is non-counting, then $\mathcal{L}(\varphi_1)$ has threshold $n_0’\in\mathbb{N}$. We choose $n_0=n’_0$
$\textbf{Case }\varphi=\bigcirc\varphi_1:$
$\hspace{1cm}$ If $\varphi_1$ is non-counting, then $\mathcal{L}(\varphi_1)$ has threshold $n_0’\in\mathbb{N}$. We choose $n_0=n’_0+1$ and try to show
$$\text{“For }n\geq n_0,\ vw^n\alpha\models\bigcirc\varphi\ \text{ if and only if }\ n\geq n_0,\ vw^{n+1}\alpha\models\bigcirc\varphi”$$
$\hspace{1cm}$ We try to perform operations on the fix length prefix $v$ as it doesn’t affect the finite loop prefix $w$. So we
$\hspace{1cm}$ need to consider whether the fix length prefix $v$ is an empty string $(\varepsilon)$, if not, we try to “peel” one cycle of
$\hspace{1cm}$ $w$ and make it so-called “fix-length” prefix.
$\hspace{1cm}$ A simple example for the operation: if there’s logic requires $b$ to be reached in the next step, then the same
$\hspace{1cm}$ logic without neXt operator $\bigcirc$ can be satisfied by removing the first letter. (if $ab\models\bigcirc\varphi$, then $b\models\varphi$)
$\hspace{1cm}\textbf{Case }\ v\neq\varepsilon:$ Thus $v=av’$ for some $a\in\Sigma,v’\in\Sigma^\ast$. We have that
$\begin{array}{lrl}
\hspace{2cm}&av’w^n\alpha&\models\bigcirc\varphi\newline
\hspace{2cm}\text{iff}&v’w^n\alpha&\models\varphi\newline
\hspace{2cm}\text{iff}&v’w^{n+1}\alpha&\models\varphi&\text{(induction hypothesis)}\newline
\hspace{2cm}\text{iff}&av’w^{n+1}\alpha&\models\bigcirc\varphi\newline
\end{array}$
$\hspace{1cm}\textbf{Case }\ v=\varepsilon:$ Thus either $w=\varepsilon$ (proved trivially), or $w=aw’$ for some $a\in\Sigma,w’\in\Sigma^\ast$. It follows that
$\begin{array}{lrl}
\hspace{2cm}&(aw’)^n\alpha&\models\bigcirc\varphi\newline
\hspace{2cm}\text{iff}&(aw’)(aw’)^{n-1}\alpha&\models\bigcirc\varphi\newline
\hspace{2cm}\text{iff}&w’(aw’)^{n-1}\alpha&\models\varphi\newline
\hspace{2cm}\text{iff}&w’(aw’)^{n}\alpha&\models\varphi&\text{(induction hypothesis)}\newline
\hspace{2cm}\text{iff}&(aw’)^{n+1}\alpha&\models\bigcirc\varphi\newline
\end{array}$
$\textbf{Case }\varphi=\varphi_1\ \mathcal{U}\ \varphi_2:$
$\hspace{1cm}$ If $\varphi_1$ and $\varphi_2$ are non-counting, then $\mathcal{L}(\varphi_1)$ and $\mathcal{L}(\varphi_2)$ have threshold $n_0’$ and $n’’_0\in\mathbb{N}$ respectively. We
$\hspace{1cm}$ choose $n_0=\text{max}\lbrace n’_0,n’’_0\rbrace+1$ and try to show
$$”\text{For }n\geq n_0,\ vw^n\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2\ \text{ if and only if }\ vw^{n+1}\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2”$$
$\hspace{1cm}$ By the semantics of $\mathcal{U}$, $\varphi_1$ keeps holding until $\varphi_2$ is satisfied. Let $j$ be the least index when $\varphi_2$ is satisfied,
$\hspace{1cm}$ then we have $vw^n\alpha[j,\infty]\models\varphi_2$ and for all $i<j,\ vw^n\alpha[i,\infty]\models\varphi_1$, respectively applies on $vw^{n+1}\alpha$.
$\hspace{1cm}$ $\textbf{1. }\textit{If }\ vw^n\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2\textit{, then }\ vw^{n+1}\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2:$
$\hspace{2cm}$ Similar to $\bigcirc\varphi$, we try to do the operation with respect to $j$’s position. So we need to consider whether
$\hspace{2cm}$ index $j$ lies within the first cycle of the prefix $|v|+|w|$, or lies in the finite loop of the prefix $|w|$.
$\hspace{2cm}\textbf{Case }j\leq|v|+|w|:$
$\hspace{3cm}$ By induction hypothesis, we assumed $\varphi_1$ and $\varphi_2$ are non-counting. So
$\hspace{3cm}$ if $vww^{n−1}\alpha[j,\infty]\models\varphi_2$, then $vww^{n}\alpha[j,\infty]\models\varphi_2$ and analogously,
$\hspace{3cm}$ if $vww^{n−1}\alpha[i,\infty]\models\varphi_1$, then $vww^{n}\alpha[i,\infty]\models\varphi_1$ for $i < j$.
$\hspace{3cm}$ Hence, $vw^{n+1}\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2$.
$\hspace{2cm}\textbf{Case }j>|v|+|w|:$
$\hspace{3cm}$ By adding one more cycle, we can essentially get the same suffix if $j$ is somewhere in the cycle:
$\hspace{3cm}$ if $vw^{n}\alpha[j,\infty]\models\varphi_2$, then $vw^{n+1}\alpha[j+|w|,\infty]\models\varphi_2$, and
$\hspace{3cm}$ if $vw^{n}\alpha[i,\infty]\models\varphi_1$, then $vw^{n+1}\alpha[i,\infty]\models\varphi_1$, for each position $|v|+|w|\leq i<j+|w|$.
$\hspace{3cm}$ Additionally, by induction hypothesis from the above case, we have that
$\begin{array}{lrcccll}
\hspace{4cm}&|v|+|w|&\leq&i&<&j+|w|\newline
\hspace{4cm}\text{iff}&|v|&\leq&i&<&j\newline
\hspace{4cm}\text{iff}&&&i&<&j&&(\text{induction hypothesis: }i<|v|+|w|)\newline
\end{array}$
$\hspace{3cm}$ Hence, $vw^{n}\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2$.
$\hspace{1cm}$ $\textbf{2. }\textit{If }\ vw^{n+1}\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2\textit{, then }\ vw^{n}\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2:$
$\hspace{2cm}$ Again, we need consider both cases seperately:
$\hspace{2cm}\textbf{Case }j\leq|v|+|w|:$
$\hspace{3cm}$ By induction hypothesis, we assumed $\varphi_1$ and $\varphi_2$ are non-counting. So
$\hspace{3cm}$ if $vww^{n}\alpha[j,\infty]\models\varphi_2$, then $vww^{n-1}\alpha[j,\infty]\models\varphi_2$ and analogously,
$\hspace{3cm}$ if $vww^{n}\alpha[i,\infty]\models\varphi_1$, then $vww^{n-1}\alpha[i,\infty]\models\varphi_1$ for $i < j$.
$\hspace{3cm}$ Hence, $vw^{n}\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2$.
$\hspace{2cm}\textbf{Case }j>|v|+|w|:$
$\hspace{3cm}$ Simliar to above, by subtracting one more cycle, we can essentially get the same suffix:
$\hspace{3cm}$ if $vw^{n+1}\alpha[j,\infty]\models\varphi_2$, then $vw^{n}\alpha[j-|w|,\infty]\models\varphi_2$, and
$\hspace{3cm}$ if $vw^{n+1}\alpha[i,\infty]\models\varphi_1$, then $vw^{n}\alpha[i,\infty]\models\varphi_1$, for each position $|v|+|w|\leq i<j-|w|$.
$\hspace{3cm}$ Again, by induction hypothesis from the above case, we have that
$\begin{array}{lrcccll}
\hspace{4cm}&|v|+|w|&\leq&i&<&j-|w|\newline
\hspace{4cm}\text{iff}&|v|+2|w|&\leq&i&<&j\newline
\hspace{4cm}\text{iff}&&&i&<&j&&(\text{induction hypothesis: }i<|v|+|w|)\newline
\end{array}$
$\hspace{3cm}$ Hence, $vw^{n}\alpha\models\varphi_1\ \mathcal{U}\ \varphi_2$.
Summary
Unfortunately, LTL is not expressive enough to include all $\omega$-regular languages. However, by extending the syntax of LTL, we can also extend the languages it covers.
In the next section, we will Quantified Propositional Temporal Logic (QPTL), and see whether it suffices to solve our problem.
Next chapter: Quantified Propositional Temporal Logic (QPTL)
Please cite the source for reprints, feel free to verify the sources cited in the article, and point out any errors or lack of clarity of expression. You can comment in the comments section below or email to GreenMeeple@yahoo.com