AGV 6.7 -- S1S$_0$ and Büchi-recognizable Language

Notes > UdS AGV

Created At : 2024-11-29 00:36

Count:1.1k Views :

Introduction
From S1S to S1S$_0$
1. Proof
From S1S-definable to Büchi-recognizable
1. Proof

Previous chapter: Express QPTL using S1S

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

To prepare for the proof that every S1S-definable language is Büchi-recognizable, we show in the following lemma that we can focus on a restricted sublogic, called S1S$_0$, which is defined by the following grammar:

$$\varphi::=0\in X\mid x\in Y\mid x=0\mid x=y\mid x=S(y)\mid \neg\varphi\mid\varphi\wedge\varphi\mid\exists x.\varphi\mid\exists X.\varphi$$

Membership tests $(\in)$: variables $(x,y,\dots)$ and $0$ only
Equalities $(=)$: variables $(x,y,\dots)$, $0$ and a single successor operation $(S(t))$ only
- i.e. $S(S(t))$ is not allowed.

Complex formula in S1S can then be simplified by introducing additional variables.

From S1S to S1S$_0$

$\textbf{Lemma 6.1. } \textit{For every S1S formula }\varphi\textit{ there is an S1S}_0\text{ formula }\varphi’\textit{ such that }\mathcal{L}(\varphi)=\mathcal{L}(\varphi’).$

Proof

We rewrite a given S1S formula $\varphi$ into the S1S$_0$ formula $\varphi$’ using the following rewrite rules:

S1S	S1S_0	Explanation
$S(t)\in X$	$\exists y. y=S(t)\wedge y\in X$	only $0$ and `First-order variable` $(x,y,\dots)$ is allowed on the L.H.S of $\in$
$0=x$	$x=0$	`First-order variable` has higher priority than $0$
$S(t)=0$	$0=S(t)$	successor operation not allowed on L.H.S
$S(t)=x$	$x=S(t)$	successor operation not allowed on L.H.S
$S(t)=S(t’)$	$t=t’$	successor operation not allowed on L.H.S
$0=0$	$\exists Y.0\in Y\vee0\notin Y$	only accept the form $x=0$
$0=S(t)$	$\exists y.y=S(t)\wedge y=0$	only accept the form $x=0$ or $x=S(y)$
$t=S(0)$	$\exists x.x=0\wedge t=S(x)$	only accept the form $x=S(y)$
$t=S(S(t’)$	$\exists y.y=S(t’)\wedge t=S(y)$	only allow one successor operation

From S1S-definable to Büchi-recognizable

$\textbf{Theorem 6.4. } \textit{Every S1S-definable language is Büchi-recognizable.}$

Proof

Let $\varphi$ be an S1S-formula. We construct a Büchi automaton $\mathcal{A}$ with $\mathcal{L}(\varphi)=\mathcal{L}(\mathcal{A})$.

Step 1: We begin by translating $\varphi$ into an equivalent S1S$_0$ according to the above Lemma 6.1.
Step 2: Express every basic S1S$_0$ formula from the grammar above using Büchi automaton.

Remember in last section, when we translate QPTL to S1S, we defined Second-order variable $X$ as atomic proposition of QPTL. Here same definitions continue:

First of all, $A$ is the set of atomic propositions $(A\subseteq AP)$ which is avaliable in the current state. For example, in state $q_2$, $A = \lbrace X,Y\rbrace$, where $AP = \lbrace X,Y,Z\rbrace$. Which means in $q_2$ there exists transitions only when proposition $X$ or $Y$ is $\textit{true}$.

Then, words are defined as a sequence containing atomic propositions. For example, a possible structure for word $\alpha$ may look like this: $$\alpha=\lbrace XYYXXYY\dots\rbrace$$

Finally, our definition of Second-order variable is set of positions, and First-order variable are the positions. The relationship between proposition and variables in S1S is essentially $\alpha[x] = X$, where $x$ is some First-order variable and $X$ is some Second-order variable.

We can also use the S1S way to interpret, that proposition $X$ holds $\textit{true}$ in position x and y, i.e. $X=\lbrace x,y\rbrace$.

Therefore, when we see transitions like $\lbrace A\mid X\in A\rbrace$, it means if $X$ is part of the avaliable propositions for the current state and holds in certain letter(position), then the automata can take this transition as a path. (Here the position is not specified, will see more examples below)

$0\in X$: This statement holds $\textit{true}$ iff. theres a word that contains $X$ in zero position.
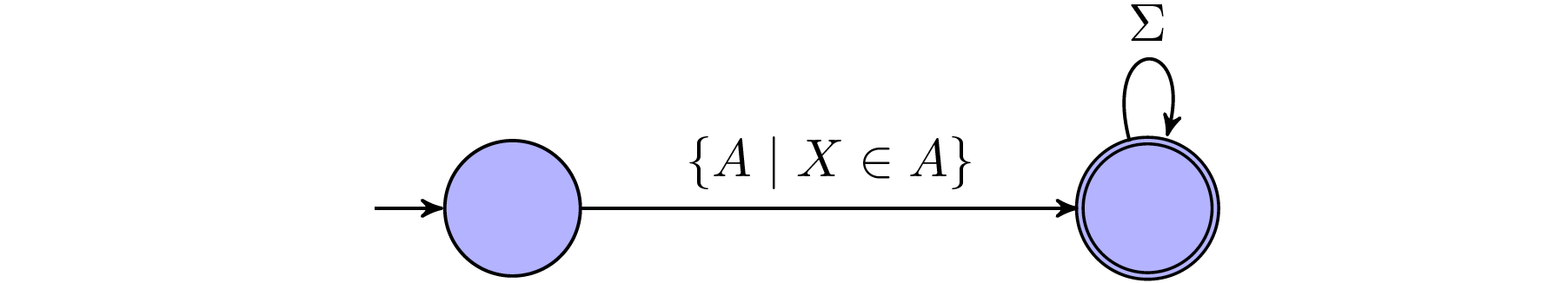
$x\in Y$: This statement holds $\textit{true}$ iff. theres a word that contains $Y$ in $x$ position.
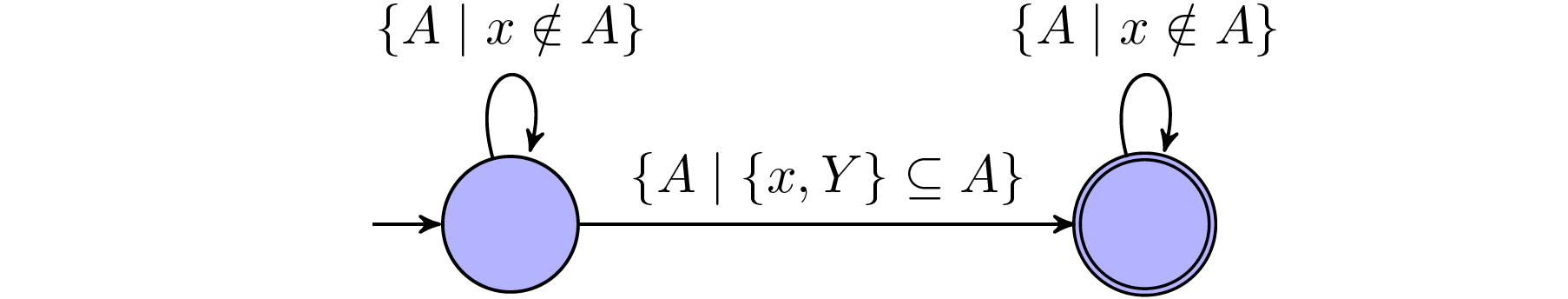
$x=0$: This statement holds $\textit{true}$ iff. the word exist some propositions that only holds $\textit{true}$ in $x$-th position, assign $x$ as $0$.
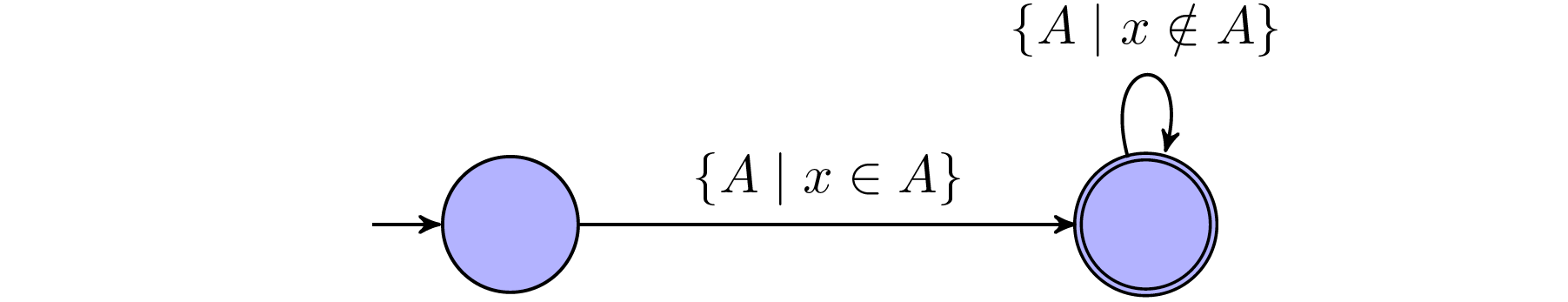
$x=y$: This statement holds $\textit{true}$ iff. the word exist some propositions that only holds $\textit{true}$ in $x$-th and $y$-th position, which are indeed the same.
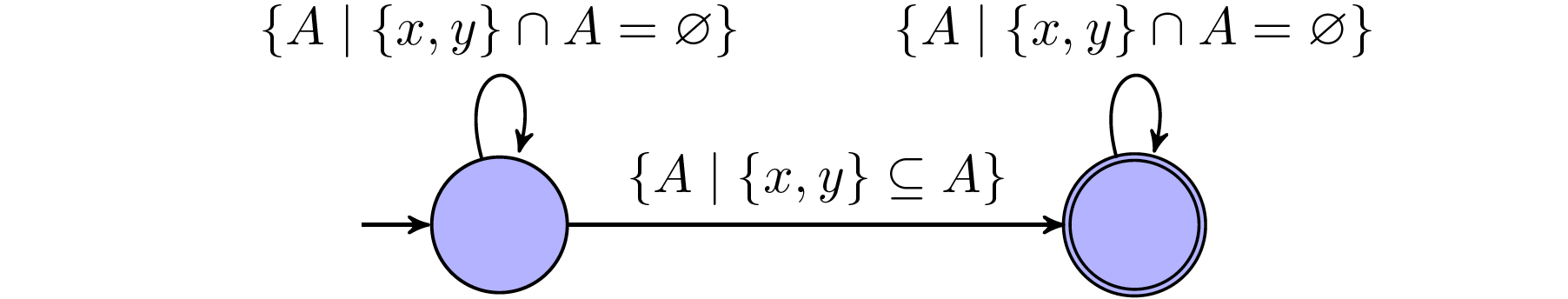
$x=S(y)$: This statement holds $\textit{true}$ iff. the word exist some propositions that only holds $\textit{true}$ in $x$-th and $y$-th position, where $x$ and $y$ are different and $x$ is the next position after $y$.
$\varphi\wedge\psi$: Let $\mathcal{A_\varphi}$ and $\mathcal{A_\psi}$ be the automata constructed for $\varphi$ and $\psi$, respectively. We obtain the automaton $\mathcal{A}_{\varphi\wedge\psi}$ by constructing the automaton that recognizes the intersection of $\mathcal{L(A_\varphi)}$ and $\mathcal{L(A_\psi)}$.
Below is the example of $0\in X \wedge x \in Y$:
$\neg\varphi$: let $\mathcal{A_{\varphi}}$ be the automaton constructed for $\varphi$. We obtain the automaton $\mathcal{A_{\neg\varphi}}$ by first constructing the automaton that recognizes the complement of $\mathcal{L(A_{\varphi})}$ and then intersecting it with $A_x$ for each free first-order variable $x$, which ensures that $x$ appears exactly once. Below we use $\neg(x\in Y)$ as an example: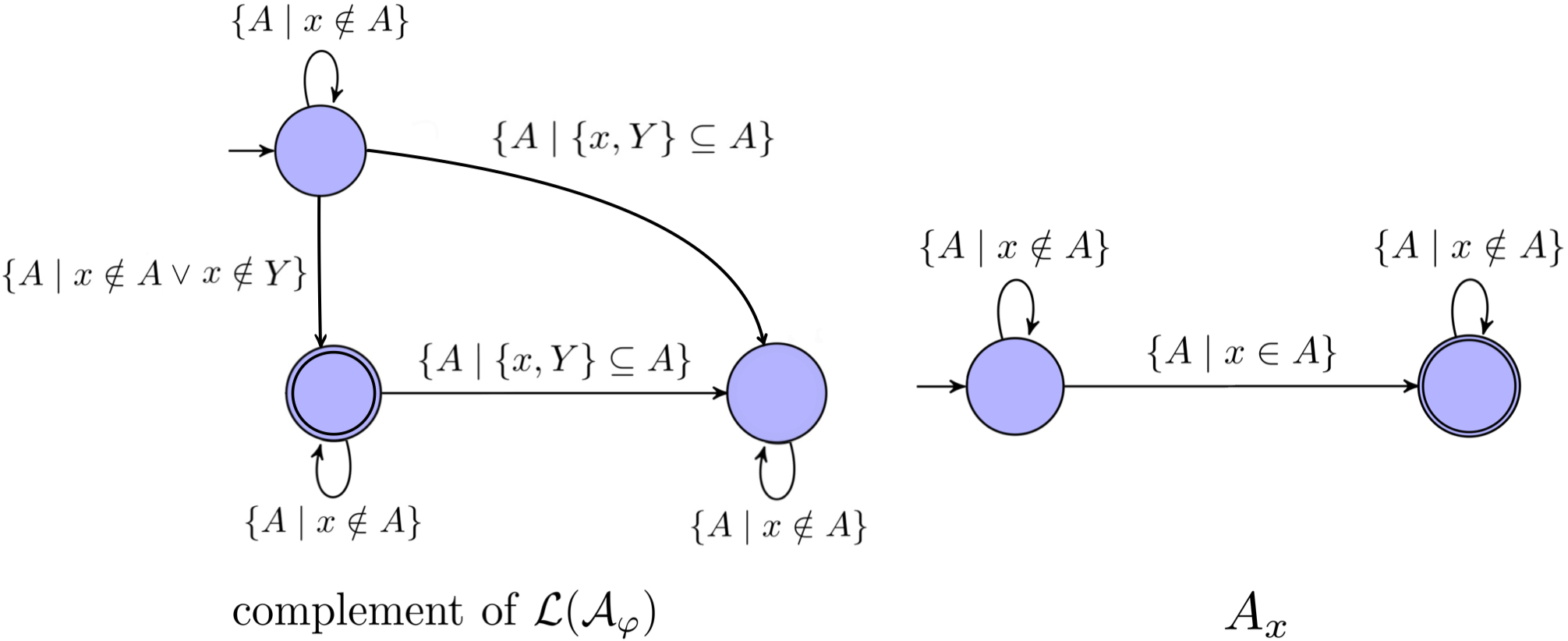

Notice that $(\lbrace x,Y\rbrace\subseteq A)\wedge(x\in A)=\lbrace x,Y\rbrace\subseteq A$: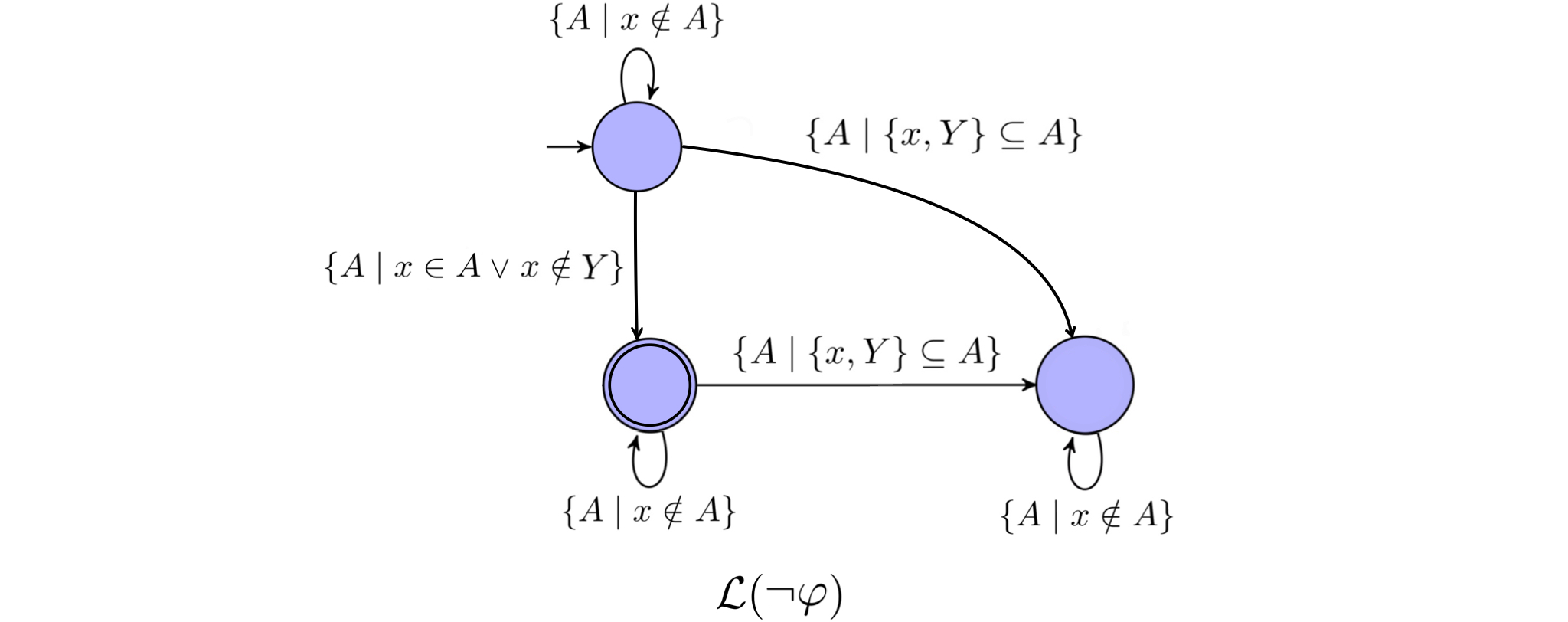
$\exists X.\varphi$: Let $\mathcal{A_{\varphi}}$ be the automaton constructed for $\varphi$. We obtain the automaton $\mathcal{A}_{\exists X. \varphi}$ for by eliminating $X$ from the input alphabet, i.e., we replace each transition $(q,A,q’)$ by $(q,A\setminus\lbrace X\rbrace,q’)$.
(Because the Büchi-recognizable Language only contains the set of free atomic propositions)
$\exists x. \varphi$: Similarly, we replace each transition $(q,A,q’)$ by $(q,A\setminus\lbrace x\rbrace,q’)$.

Next chapter: Alternating Büchi Automata