AGV 7.1 -- Alternating Büchi Automata

Notes > UdS AGV

Created At : 2024-11-30 02:25

Count:952 Views :

Introduction
Alternating Automata

Previous chapter: S1S$_0$ and Büchi-recognizable Language

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

Logics are often significantly more concise than automata. For example, in the translation from S1S to Büchi automata in the proof of Theorem 6.4, each negation increases the size of the Büchi automaton exponentially, resulting in a non-elementary number of states. The blow-up when translating LTL formulas is less dramatic, but still exponential. In this section, we show that the conciseness of the logic and the automata can be brought closer together when the automata are equipped with both nondeterministic and universal choices.

Alternating Automata

Nondeterministic and Universal

In previous sections, we discussed a lot about Nondeterministic transitions. Here we introduce a new concept Universal transitions for our new automaton called alternating automaton. We allow for both types of choices by defining, for each state and input letter, a positive Boolean formula over the successor states.

Choices	Symbol	Definition
Nondeterministic	disjunction $(\vee)$	the suffix of an input word is accepted by SOME successor state
Universal	conjunction $(\wedge)$	the suffix of an input word is accepted by ALL successor states

Positive Boolean Formulas $\ \mathbb{B}^+(X)$

$\textbf{Definition 7.1. } \text{The }\textit{positive Boolean formulas }\text{over a set }X\text{, denoted }\mathbb{B}^+(X)\text{, are the formulas}\newline\text{built from elements of }X\text{, conjunction }\wedge\text{, disjunction }\vee,\textit{ true}\text{ and }\textit{false.}$

In our automata construction, elements of $X$ will be states. Let say we have a set of states $Y\subseteq X$.
We denote $Y\models\varphi$ if $Y$ satisfies a formula $\varphi\in\mathbb{B^+}(X)$. In other words:

all states in $Y$ will be assigned as $\textit{true}$ by $\varphi$, and
all states in $X\setminus Y$ will be assigned as $\textit{false}$ by $\varphi$.

Trees and Runs

$\textbf{Definition 7.2. } \text{ An } \textit{Alternating automaton over infinite words }\mathcal{A}\newline\text{ is a tuple }\mathcal{A} = (\Sigma,Q,q_0,\delta,Acc)\text{, where}\newline\begin{array}{ll}
\hspace{1cm} \cdot \ Q &\text{ is a finite set of states} \newline
\hspace{1cm} \cdot \ q_0 \in Q& \text{ is the initial states} \newline
\hspace{1cm} \cdot \ \delta:Q\times\Sigma\rightarrow\mathbb{B^+}(Q)& \text{ is the } \textit{transition functions}\text{, and} \newline
\hspace{1cm} \cdot \ Acc \subseteq Q^\omega& \text{ is an accepting condition.}
\end{array}$

For alternating automata, runs generalize from sequences to trees. Here we define a tree as a prefix-closed subset, guarantees that all nodes must be able to trace all the back the root of the tree.

prefix-closed subset:
If a word $w=\lbrace ab\rbrace^\omega$ is in the set, then all its prefix (i.e. $\lbrace ab\rbrace,\lbrace aba\rbrace,\lbrace abab\rbrace,\dots$) must also be in the set.

Name	Symbol/Functions	Definition
Set of Squences	$D^\ast$	All possible sequence of every word by direction $D$
Set of Directions	$D$	Branches possible in each node
Tree	$\mathcal{T}$	Sequence of ONE word, a prefix-closed subset of $D^*$
Root	$\varepsilon$	The Empty Sequence
Node	$n\in\mathcal{T}$	Depends on the label, it may be the states or the letters
Children of $n$	$\text{children}(n)=\lbrace n\cdot d\in \mathcal{T}\mid d\in D\rbrace$	Succssor states of $n$ over direction $d$
$Q$-labeled tree	$(\mathcal{T},\ell)$	A tree that labels nodes with the states
$\Sigma$-labeled tree	$(\mathcal{T},\ell)$	A tree that labels nodes with the input letters
Labeling Function	$\ell:\mathcal{T}\rightarrow\Sigma$	Label each node of the tree with the input letters for $\Sigma$-labeled tree

Below, we define a run of an alternating autoamton using $Q$-labeled tree:

$\textbf{Definition 7.3. } \text{ A } \textit{run }\text{of an alternating automaton on a word }\alpha\in\Sigma^\omega\newline\text{ is a Q-labeled tree (T , r) with the following properties:}\newline
\begin{array}{l}
\hspace{1cm} \cdot \ r(\varepsilon)=q_0\text{ and}\newline
\hspace{1cm} \cdot \ \text{for all }n\in\mathcal{T}\text{, if }r(n)=q\text{, then }\lbrace r(n’)\mid n’\in\text{children}(n)\rbrace\ \text{ satisfies }\delta(q,\alpha(|n|)).
\end{array}$

Example

The following alternating Büchi automaton recognizes the language $L=((a+b)^\ast b)^\omega$. Universal choice $(\wedge)$ are depicted by connecting the edges with a small arc $(\blacksquare)$. The transition function $(\delta)$ is given as follows:

$\delta(p,a)=p\wedge q$,
$\delta(p,b)=p$,
$\delta(q,a)=q$,
$\delta(q,b)=\textit{true}$.

On the input word $\alpha=(aab)^\omega$, our automaton has the following run. Note that, in general, an alternating automaton may have more than one run on a particular word, or also no run at all. We use a dotted line to indicate that the subtree repeats infinitely often.

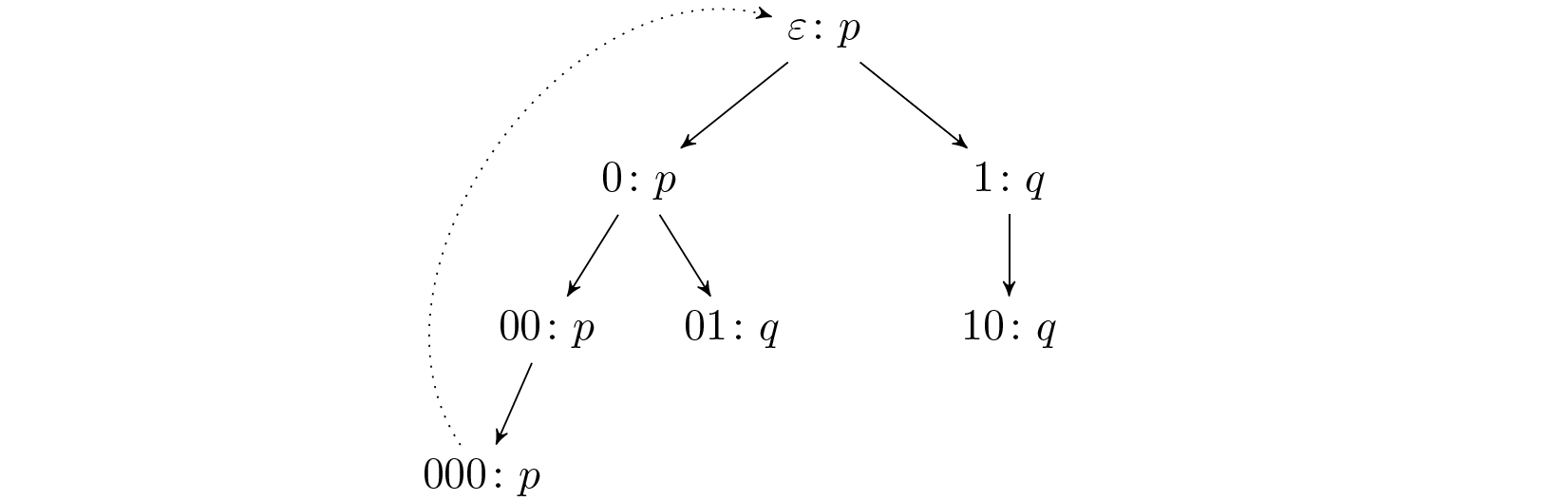
Similar to DAG, we can apply the acceptance condition only on all infinite branches of the run tree. A branch of a tree $\mathcal{T}$ is a maximal sequence of words $n_0n_1n_2\dots$ such that $n_0=\varepsilon$ and $n_{i+1}$ is a child of $n_i$ for $i\geq0$.

Obviously, if every infinite branch is accepting, then the entire tree is thus accepting, i.e. there’s no way to pick a non-accepting path for to be the run.

$\textbf{Definition 7.4. } \text{A run }(\mathcal{T},r)\text{ is }\textit{accepting }\text{iff, for every infinite branch }n_0n_1n_2\dots,$
$$r(n_0)r(n_1)r(n_2)\dots\in Acc.$$

Next chapter: From LTL to Alternating Büchi Automata