AGV 7.2 -- From LTL to Alternating Büchi Automata

Notes > UdS AGV

Created At : 2024-12-01 03:08

Count:895 Views :

Introduction
From LTL to Alternating Automata
Explanation and Examples in Human language
1. Proof

Previous chapter: Alternating Büchi Automata

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

It is usually much simpler to translate a logical formula into an alternating automaton than into a nondeterministic automaton. We illustrate this with the translation of LTL formulas into equivalent alternating Büchi automata. The states are simply the subformulas of the given formula and their negations (this set is called the closure of the formula). The transition function is derived from the expansion laws of the logic.

For example, an Until formula $\varphi_1\ \mathcal{U}\ \varphi_2$ holds if:

$\varphi_2$ holds or
$\varphi_1$ holds and the entire formula holds in the next step.

The boolean formula produced by the transition function from the state $\varphi_1\ \mathcal{U}\ \varphi_2$ is therefore:

a disjunction $(\wedge)$ between the transition function for $\varphi_2$ and
a conjunction $(\vee)$ between the transition function for $\varphi_1$ and the state $\varphi_1\ \mathcal{U}\ \varphi_2$.

From LTL to Alternating Automata

$\textbf{Construction 7.1. }\text{Let }\varphi\text{ be an LTL formula. We construct the alternating Büchi automaton }\newline\mathcal{A_\varphi}=(\Sigma,Q,\varphi,\delta,\small\text{BÜCHI} \normalsize(F))\text{ using:}$
$\begin{array}{ll}
\hspace{0.5cm} \cdot \ Q = \text{closure}(\varphi):=\lbrace\psi,\neg\psi\mid\psi\text{ is subformula of }\varphi\rbrace \newline
\hspace{0.5cm} \cdot \ \delta(p,a)= \left\lbrace \begin{array}{ll}\textit{true}&\text{if }p\in a\newline \textit{false}&\text{if }p\not\in a\end{array}\right. &\cdot \ \delta(\neg\psi,a)=\overline{\delta(\psi,a)}\newline
\hspace{0.5cm} \cdot \ \delta(\psi_1\wedge\psi_2,a)=\delta(\psi_1,a)\wedge\delta(\psi_2,a) &\cdot \ \delta(\psi_1\vee\psi_2,a)=\delta(\psi_1,a)\vee\delta(\psi_2,a)\newline
\hspace{0.5cm} \cdot \ \delta(\psi_1\ \mathcal{U}\ \psi_2,a)=\delta(\psi_2,a)\vee(\delta(\psi_1,a)\wedge\psi_1\ \mathcal{U}\ \psi_2)&\cdot \ \delta(\bigcirc\psi,a)=\psi\newline
\hspace{0.5cm} \cdot \ F = \lbrace\neg(\psi_1\ \mathcal{U}\ \psi_2)\in\text{clousure}(\varphi)\rbrace
\end{array}\newline$
$\text{where we define }\overline{\varphi}=\neg\varphi\text{ for all other }\psi\in Q\text{ and }\overline{\ \cdot\ }\text{ for }\psi,\psi_1,\psi_2\in Q\text{ via:}$
$\begin{array}{ll}
\hspace{0.5cm} \cdot \ \overline{\neg\varphi}=\varphi
\hspace{0.5cm} \cdot \ \overline{\psi_1\wedge\psi_2}=\overline{\psi_1}\vee\overline{\psi_2}
\hspace{0.5cm} \cdot \ \overline{\psi_1\vee\psi_2}=\overline{\psi_1}\wedge\overline{\psi_2}
\hspace{0.5cm} \cdot \ \overline{\textit{true}}=\overline{\textit{false}}
\hspace{0.5cm} \cdot \ \overline{\textit{false}}=\overline{\textit{true}}
\end{array}$

Explanation and Examples in Human language

Remember that $\delta$ function returns set of states.

As we can see most of the function here don’t actually have a designated successor except for atomic proposition $p$, neXt $\bigcirc$, and Until $\mathcal{U}$.

For example, here are simple steps to construct a automaton for a formula $p\wedge\bigcirc q$:

List of all possible atomic propositions input: $\sigma=\lbrace\lbrace\varnothing\rbrace,\lbrace p\rbrace,\lbrace q\rbrace,\lbrace p,q\rbrace\rbrace$
Write a truth table basic on the formula and its corresponding function $\delta$:
$\ \newline\hspace{1cm}\delta(p\wedge\bigcirc q,\sigma) = \delta(p,\sigma)\wedge\delta(\bigcirc q,\sigma)=\delta(p,\sigma)\wedge q
\newline\ \newline
\hspace{1cm}\cdot \ \delta(\bigcirc q,\sigma)=\left\lbrace \begin{array}{ll}
q&\text{if }\sigma=\lbrace\varnothing\rbrace,\lbrace q\rbrace,\lbrace p\rbrace,\lbrace p,q\rbrace\end{array} \right. \newline\ \newline
\hspace{1cm}\cdot \ \delta(p,\sigma)=\left\lbrace\begin{array}{ll}
\textit{false}&\text{if }\sigma=\lbrace\varnothing\rbrace,\lbrace q\rbrace\newline
\textit{true}&\text{if }\sigma=\lbrace p\rbrace,\lbrace p,q\rbrace\end{array}\right.
\hspace{1cm}\cdot \ \delta(q,\sigma)=\left\lbrace\begin{array}{ll}
\textit{false}&\text{if }\sigma=\lbrace\varnothing\rbrace,\lbrace p\rbrace\newline
\textit{true}&\text{if }\sigma=\lbrace q\rbrace,\lbrace p,q\rbrace\end{array}\right.
\newline\ \newline\hspace{1cm}\therefore\ \delta(p\wedge\bigcirc q,\sigma)=\left\lbrace\begin{array}{ll}
\textit{false}\wedge q = \textit{false}&\text{if }\sigma=\lbrace\varnothing\rbrace,\lbrace q\rbrace\newline
\textit{true}\wedge q = q&\text{if }\sigma=\lbrace p\rbrace,\lbrace p,q\rbrace\end{array}\right.
$
Initial state is always the orginal formula, then we add extra state according to the truth table we constructed. Here, our graph have no universal or nondeterministic transitions:

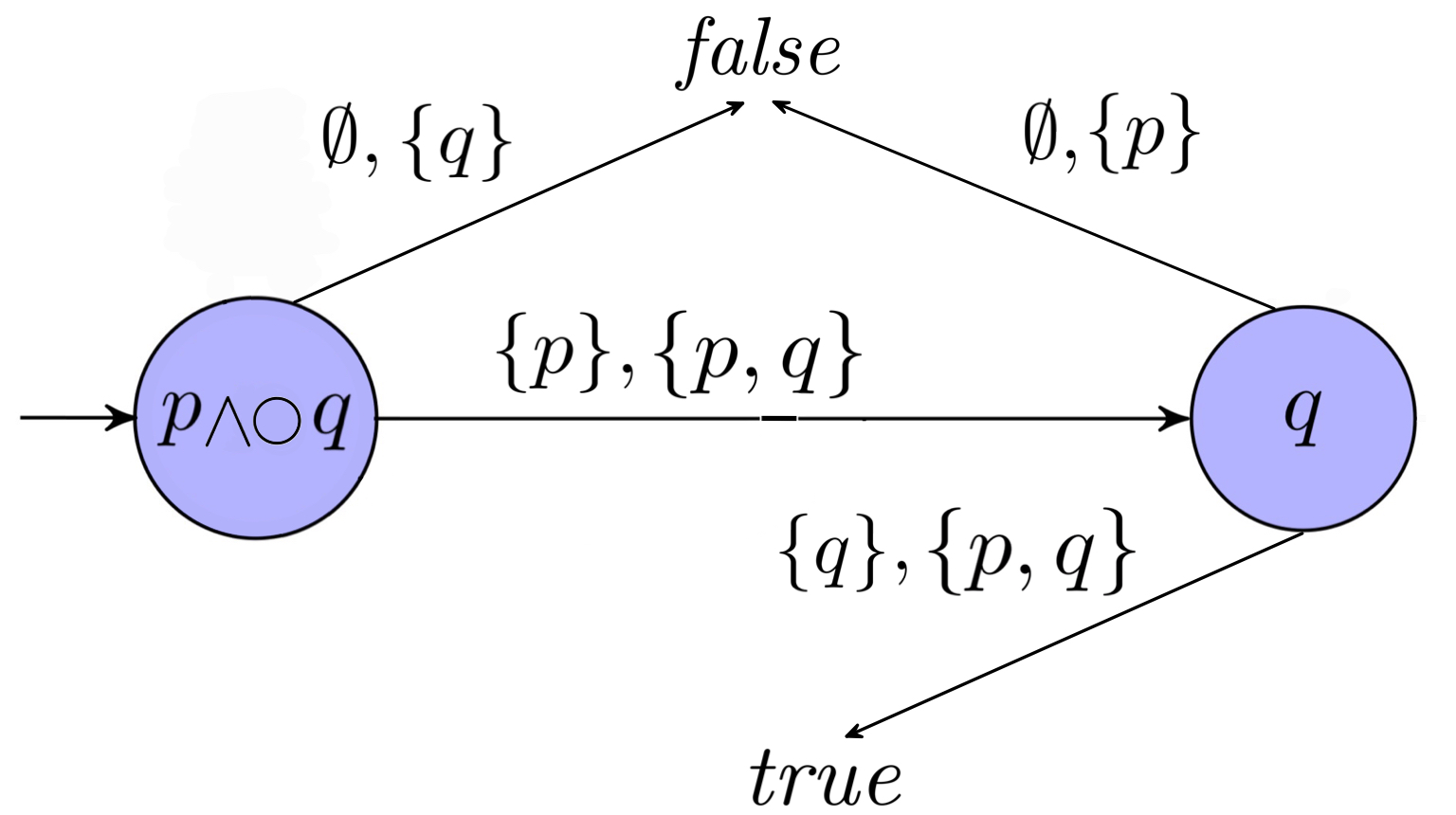
For a more complicated example, i.e. $((\Diamond p)\ \mathcal{U}\ (\square q))$, check here as an extra material

$\textbf{Theorem 7.1. } \textit{For every LTL formula }\varphi\textit{, there is an alternating Büchi automaton }\mathcal{A_\varphi}\newline\textit{with }\mathcal{L(A_\varphi)} = \mathcal{L(\varphi)}.$

Proof

We can simply prove this by induction. First, any LTL formula $\varphi$ can be recursively seperate into smaller subformula, namely $\psi$.

Similarly we can construct automaton $\mathcal{A^\psi_\varphi}$ from $\mathcal{A_\varphi}$ according to above construction 7.1. By structural induction on $\psi$, we can then prove that $\mathcal{L(A^\psi_\varphi)=L(A_\varphi)}$.

Next chapter: Translating alternating to nondeterministic automata