AGV 9.3 -- The Emerson-Lei algorithm

Notes > UdS AGV

Created At : 2024-12-10 03:56

Count:932 Views :

Introduction

Previous chapter: Nested depth-first search

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

As an alternative algorithm for checking language emptiness of Büchi automata we now discuss a classic algorithm due to Emerson and Lei. Unlike the depth-first search of the previous subsection, the Emerson-Lei algorithm is based on a breadth-first search implemented as a fixpoint construction over sets of states.

A disadvantage of this algorithm is that its running time is quadratic. Nevertheless, algorithms of this type play a major role in symbolic model checking, because the sets of states can often be represented efficiently
using data structures like binary decision diagrams.

Live states

A state $q$ of a Büchi automaton is live if some infinite path starting in $q$ visits accepting states infinitely often. This definition is the opposite of safe states, where it never visits accepting states. The idea of the algorithm is to identify the set of live states. The language of a Büchi automaton is non-empty iff it has a live initial state.

The Emerson-Lei algorithm is based on the following inductive definition:

$\textbf{Definition 9.1. } \text{For a Büchi automaton and a number }n\in\mathbb{N}\text{, the set of }\textit{n-live states}\text{ is}\newline\text{defined as follows:}$

$\begin{array}{l}
\hspace{1cm}\cdot\ \text{every state is 0-live}\newline
\hspace{1cm}\cdot\ \text{a state q is (n + 1)-live if some path containing at least one transition leads from }q\newline\hspace{1.3cm}\text{to an accepting n-live state}\newline
\end{array}$

Fixpoint

Let $\mathit{live}_n$ denote the set of $n$-live states. It is easy to see that $\mathit{live}_{n} \supseteq \mathit{live}_{n+1}$, because $\mathit{live}_{0}$ represents the set of all states in the automaton, and $\mathit{live}_{1}$ are only those which can reach the accepting states. Then $\mathit{live}_{2}$ are those who can only reach the accepting states through some states in $\mathit{live}_{1}$. Therefore set $\mathit{live}_{n+1}$ can never be larger than its previous set $\mathit{live}_{n}$.

Since the set of states is finite, there exists a fixpoint $\mathit{live}_k$ such that $\mathit{live}_k=\mathit{live}_{k+1}$. Then the set $\mathit{live}_k$ is the set of live states.

Example

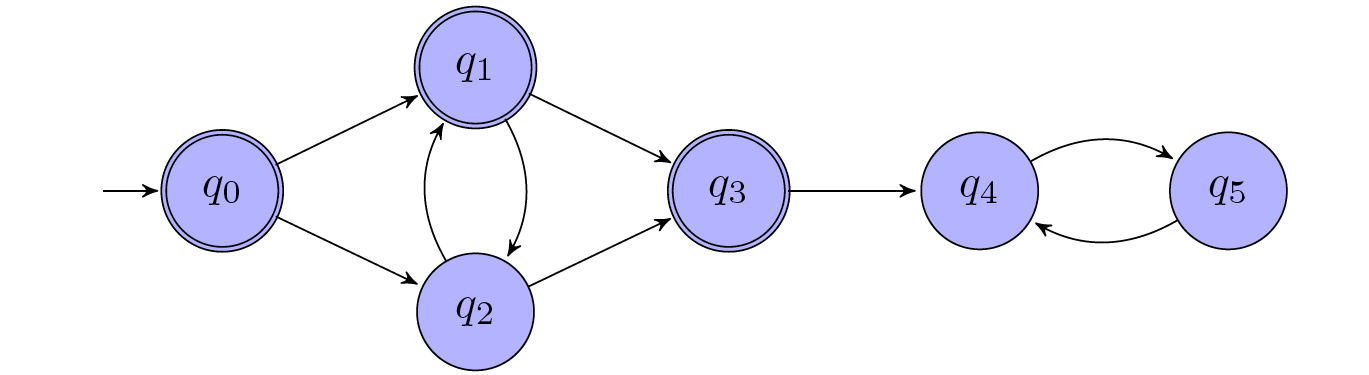
In the example from last section, states $q_0$, $q_1$ and $q_2$ are live; states $q_3$, $q_4$, and $q_5$ are only $0$-$\textit{live}$ (you cannot visit other accepting states starting from $q_3$ even though it is an accepting state).

To describe the algorithm, we first introduce a construction that implements a backward breadth-first search as a least fixpoint. The construction computes all states from which a given set of states is reachable.

$\textbf{Construction 9.1. } \text{For a Büchi Automaton }\mathcal{A} = (\Sigma,Q,I,T,\small\text{BÜCHI} \normalsize (F))\text{ and a set of states}\newline R\subseteq Q\text{, we compute the set of backwards reachable states from }R\text{ as follows:}$

$\begin{array}{llll}
\hspace{1cm} \cdot & \textit{Pre}(R)&=&\lbrace q\in Q\mid \exists q’\in R,\sigma\in\Sigma,(q,\sigma,q’)\in T\rbrace\newline
\hspace{1cm} \cdot & \textit{BackwardReach}_0(R)&=&R\newline
\hspace{1cm} \cdot & \textit{BackwardReach}_{n+1}(R)&=&\textit{BackwardReach}_{n}(R)\cup\textit{Pre}(\textit{BackwardReach}_{n}(R))\newline
\hspace{1cm} \cdot & \textit{BackwardReach}(R)&=&\underset{n\in\mathbb{N}}{\bigcup}\textit{BackwardReach}_{n}(R)\newline
\end{array}$

By this construction, it returns a set of states that can reach some states in $R$. For example, $\lbrace q_0,q_1,q_2\rbrace$ can reach $q_3$. Using this construction as a subroutine, we can compute the live states as a greatest fixpoint:

$\textbf{Construction 9.2. } \text{For a Büchi Automaton }\mathcal{A} = (\Sigma,Q,I,T,\small\text{BÜCHI} \normalsize (F))\text{ we compute the set}\newline\text{of live states as follows:}$

$\begin{array}{llll}
\hspace{1cm} \cdot & \textit{live}_0&=&Q\newline
\hspace{1cm} \cdot & \textit{live}_{n+1}&=&\textit{BackwardReach}(\textit{Pre}(\textit{live}_n\cap F))\newline
\hspace{1cm} \cdot & \textit{live}&=&\underset{n\in\mathbb{N}}{\bigcap}\textit{live}_{n}\newline
\end{array}$

The set of $\textit{live}$ is the smallest subset of all $\textit{live}_n$ in any $n\in\mathbb{N}$. Therefore the function will stop when $\mathit{live}_k$ such that $\mathit{live}_k=\mathit{live}_{k+1}$, which is the greatest fixpoint of the set of live states.

Then we can verify whether the automaton is non-empty, i.e. $q_0\in\textit{live}$.

Example (cont.)

We compute the live states as follows:

$\begin{array}{llll}
\hspace{1cm} \cdot & \textit{live}_0&=&\lbrace q_0,q_1,q_2,q_3,q_4,q_5\rbrace\newline
\hspace{1cm} \cdot & \textit{live}_1&=&\lbrace q_0,q_1,q_2\rbrace\newline
\hspace{1cm} \cdot & \textit{live}_2&=&\lbrace q_0,q_1,q_2\rbrace\newline
\hspace{1cm} \cdot & \textit{live}&=&\lbrace q_0,q_1,q_2\rbrace\newline
\end{array}$

Since the initial state $q_0$ is live, we have that the language of the automaton is non-empty.

Next chapter: The Muller Acceptance Condition