AGV 11.3 -- Büchi Games
Previous chapter: Reachability Games
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Recurrence Construction
In a Büchi game, the goal of Player 0 is to visit some accepting position infinitely often. The attractor construction checks whether there is a strategy which enforces at least one visit to an accepting position. Reaching an accepting state at least once is indeed a necessary precondition, but we also have to ensure that from this position we can enforce a second visit to some accepting state, then a third, and so forth.
The recurrence construction computes the largest subset of the accepting states from which Player 0 can enforce infinitely many subsequent visits to the subset.
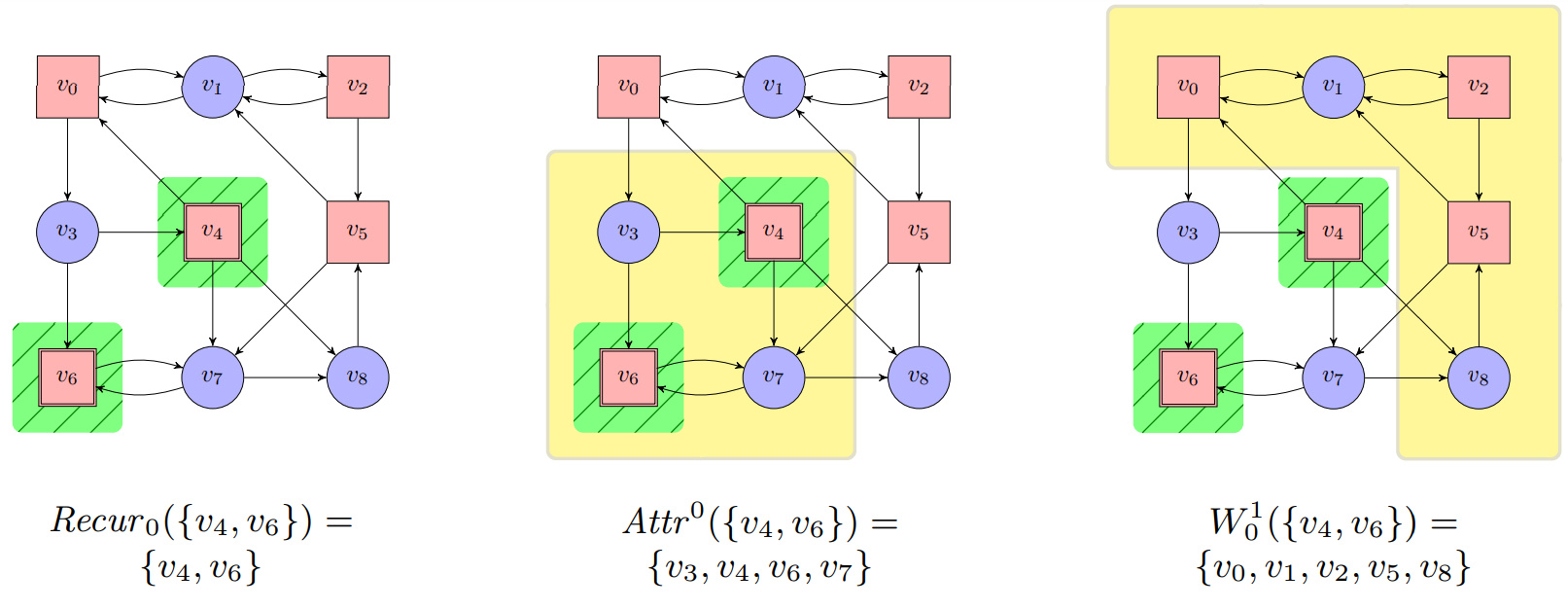
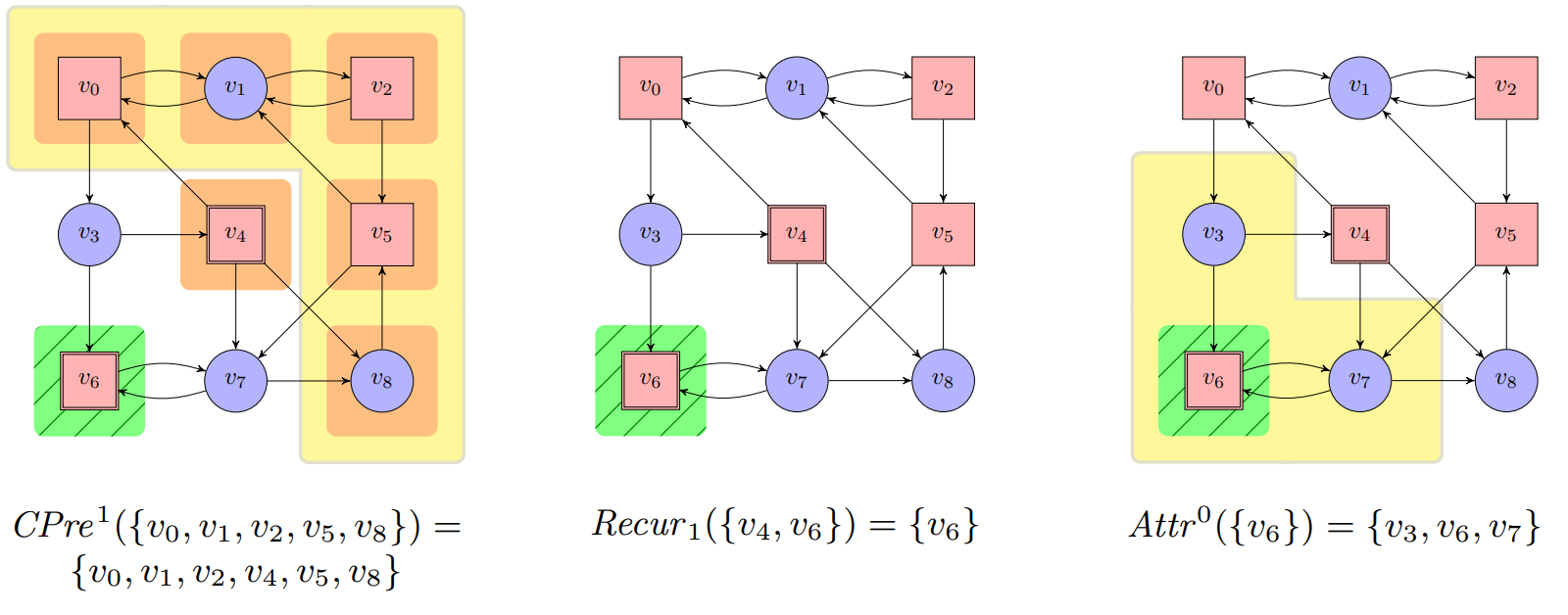
$\textbf{Construction 11.2. } \text{Let an arena }\mathcal{A} = (V_0,V_1,E)\text{ with }V=V_0\cup V_1\text{ be given. The }$ $\textit{recurrence construction}\text{ on }\mathcal{A}\text{ is defined for all }n\in\mathbb{N}\text{ and }F\subseteq V\text{ as:}$
$\begin{array}{lll} \hspace{1cm} \cdot \ W_n^1(F) &=& V\setminus Attr^0(Recur_n(F))\newline \hspace{1cm} \cdot \ Recur_{0}(F)&=&F \newline \hspace{1cm} \cdot \ Recur_{n+1}(F)&=&Recur_{n}(F)\setminus CPre^{1}(W_n^1(F)) \newline \hspace{1cm} \cdot \ Recur(F)&=&\underset{n\in\mathbb{N}}{\bigcap} Recur_{n}(R)\newline \end{array}$
The set $W_n^1(F)$ contains those positions in $V$ from which Player 1 can enforce that at most $n$ visits to $F$.
The set $CPre^{1}(W_n^1(F))$ adds those positions in $V$ from which move to positions in $W_n^1(F)$, meaning that there are at most $n+1$ visits to $F$ in newly added positions.
The set $Recur_{n}(F)$ contains the subset of $F$ from which Player 0 can enforce at least $n$ further (i.e., a total of at least $n+1$) visits to $F$.
The set $Recur(F)$ contains the subset of $F$ from which Player 0 can enforce infinitely many visits to $F$. The recurrence construction solves a game with winning condition $\small\text{BÜCHI} \normalsize (F)$ as follows:
$$
W_0(\mathcal{G})=Attr^0(Recur(F)),\ W_1(\mathcal{G})=V\setminus W_0(\mathcal{G})
$$
$$
\text{Position of Player 0: Circles;}\ \ \text{Positions of Player 1: rectangles.}$$
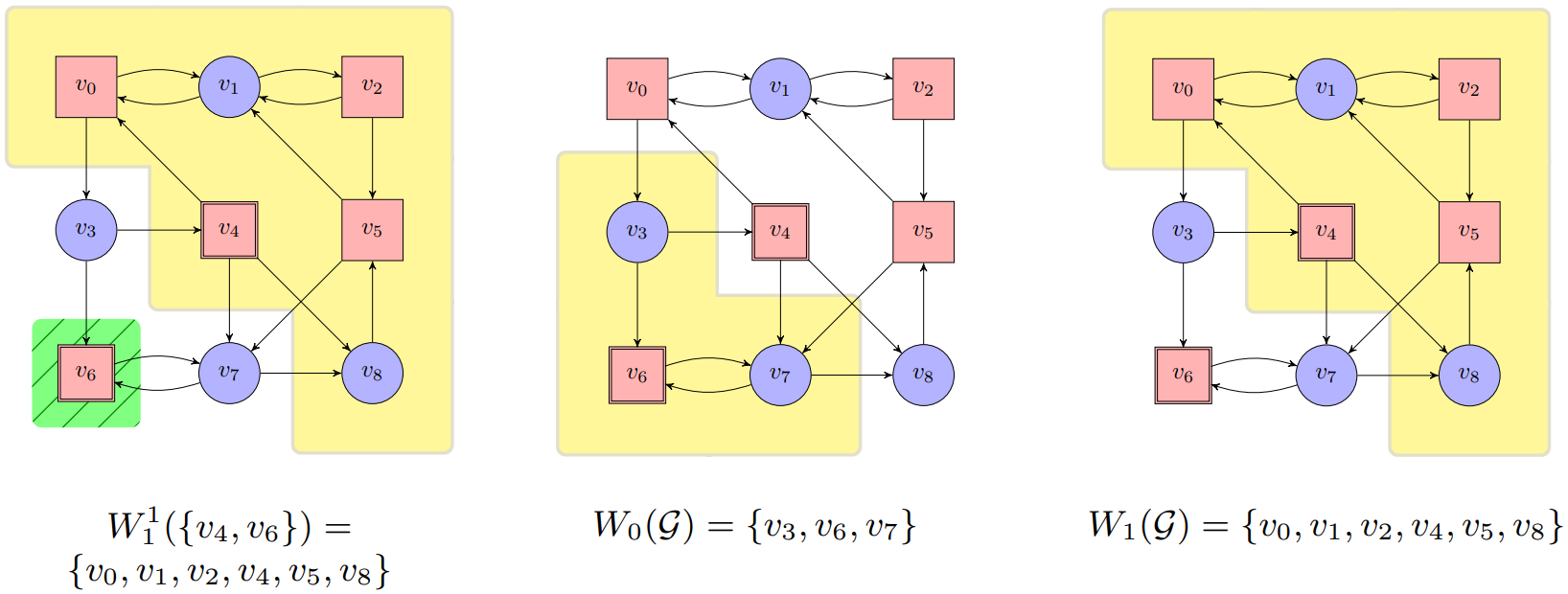
$\textbf{Theorem 11.2. } \textit{Büchi games are memoryless determined. It holds that}$ $ W_0(\mathcal{G})=Attr^0(Recur(F)), W_1(\mathcal{G})=V\setminus W_0(\mathcal{G})\textit{. Both players have a uniform winning strategy.}$
Proof
We show for all positions $v\in V$ that
If $v\in Attr^0(Recur(F))$, then $v\in W_0(\mathcal{G})$, with the following uniform memoryless strategy $\sigma$:
We fix some arbitrary total ordering on $V$. For $v\in (Attr^0(Recur(F))\setminus Recur(F))\cap V_0$, we follow the attractor strategy from the proof of Theorem 11.1.
For $v\in Recur(F)\cap V_0$, we choose the smallest $v’\in V$ with $(v,v’)\in E$ and $v’\in Attr^0(Recur(F))$. Such a successor must exist, because otherwise $v\in CPre^{1}(W_n^1(F))$ for some $n\in\mathbb{N}$, and hence $v\notin Recur(F)$.
Every play that is consistent with $\sigma$ visits $Recur(F)\subseteq F$ infinitely often. Hence, $\sigma$ is winning for Player 0.
If $v\in V\setminus Attr^0(Recur (F))$, then $v\in W_1(\mathcal{G})$, with the following uniform memoryless strategy $\tau$:
We again fix an arbitrary total ordering on $V$. We define the memoryless strategies $\tau$ such taht, for $n\in\mathbb{N}$, if a play starts in $v\in W_n^1=V\setminus Attr^0(Recur_n(F))$ and is consistent with $\tau$, there are at most $n$ visits to $F$.
For $n=0$ let $\tau(v)$ be the smallest $v’\in V$ such that $(v,v’)\in E$ and $v’\in V\setminus Attr^0(F)$.
For $n>0$ let $\tau(v)$ be the smallest $v’\in W_{n-1}^1(F)$ with $(v,v’)\in E$ if $v\in CPre^1(W_{n-1}^1(F))$, otherwise be the smallest $v’$ in $W_{n}^1(F)$ with $(v,v’)\in E$. Such a $v’$ always exists as otherwise $v\in Attr^0(Recur (F))$.
Explaination
Strategy for Player 0
If a position $v$ belongs to $(Attr^0(Recur(F))\setminus Recur(F))\cap V_0$, it must have edges to $Recur(F)$, then choose the smallest $v’$ among those.
If a position $v$ belongs to $Recur(F)\cap V_0$, we need to ensure it will visit $F$ again, so we need to choose an edge that belongs to $Attr^0(Recur(F))$.
Strategy for Player 1
Every position from Player 1 must belong to $W_n^1$, that ensures that only at most n times visits to $F$, otherwise Player 1 has no choice (belongs to $Attr^0(F)$)
For such $n = 0$, we can ensure it never visit $F$ by choosing smallest $v’$ that does not move to $Attr^0(F)$.
For such $n > 0$, if $v$ belongs to $W_{n-1}^1$, then it must have edge(s) that also belongs to $W_{n-1}^1$, otherwise there exist edge(s) belongs to $W_{n}^1$, so that it can stays in winning region of Player 1 without visiting $Attr^0(F)$.
Next chapter: Parity Games
AGV 11.3 -- Büchi Games