AGV 11.4 -- Parity Games

Previous chapter: Büchi Games

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

Perhaps the most intriguing type of infinite games are parity games. Parity games play a key role in verification (in particular for $\mu$-calculus model checking) and synthesis, and finding fast algorithms for parity games is an active research topic.

The algorithm discussed in the following takes exponential time. There are also several quasi-polynomial-time algorithms for solving parity games (starting with a breakthrough result by Calude, Jain, Khoussainov, Li, and Stephan in 2017). In practice, however, these algorithms do not perform well (yet).

Parity Condition

$\mathbf{\text{Definition 11.10. }}\text{The }\mathit{\text{parity condition }}\text{PARITY}(C)\text{ for a coloring function }c:V\to \mathbb{N}\text{ is the set}$
$$\text{PARITY}(C)=\{\alpha \in V^{\omega }\mid \text{max}\{c(q)\mid q\in \text{Inf}(\alpha )\}\text{is even}\}.$$

The parity condition is satisfied if the biggest number $q$ of the coloring function is even, among all positions that are visited infinitely often.

Example

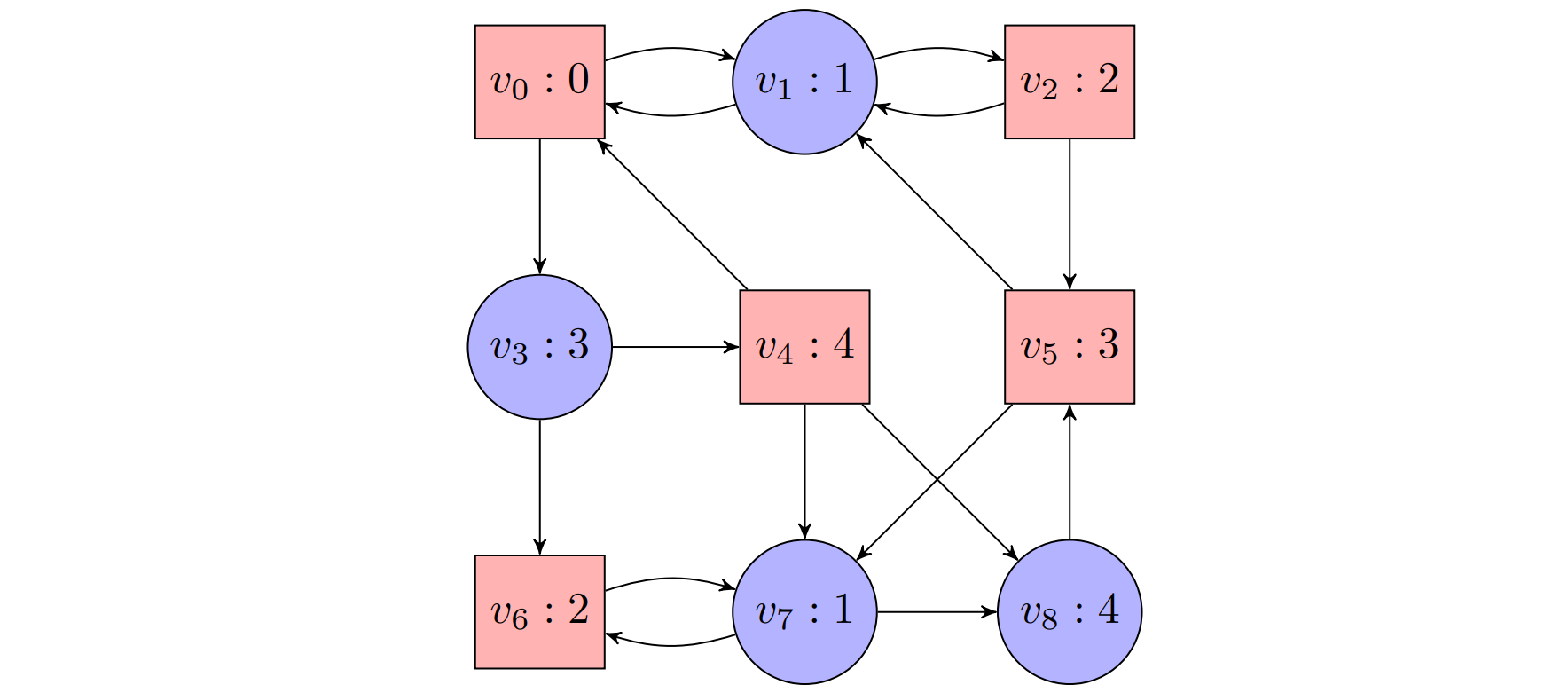
• The winning region for Player 0: $W_0(\mathcal{G})=\{v_3,v_6,v_7\}$

  • Strategy: $\sigma (v_3)=v_6,\sigma (v_7)=v_4,\sigma (v_7)=v_6$ ($v_8$ have no choices and $v_1$ is arbitrary)

• The winning region for Player 1: $W_1(\mathcal{G})=\{v_0,v_1,v_2,v_4,v_5,v_8\}$

  • Strategy: $\tau (v_0)=v_1,\tau (v_2)=v_5,\tau (v_4)=v_0,\tau (v_5)=v_1$

We first prove that parity games are memoryless determined, then derive an algorithm for solving parity games. In the following theorem, we emphasize that determinacy holds also for (countably) infinite game arenas.

This will be helpful when we use the determinacy to complement tree automata, because the acceptance game of a tree automaton refers to the infinite input tree and is therefore infinite.

$$\begin{gathered} \mathbf{\text{Theorem 11.3. }}\mathit{\text{Parity games are memoryless determined with uniform winning strategies}} \\ \mathit{\text{for game arenas with a countable set of positions and a finite number of colors.}} \end{gathered}$$

Here, we try to construct a uniform winning strategy for an arbitrary parity game.

Proof

Let $k=\text{max}\{c(v)\mid v\in V\}$ be the highest color in the given parity game. We prove that parity games are memoryless determined by induction on $k$.

Case $k=0$: If the highest color is 0, then all plays are winning. $W_0(\mathcal{G})=V,W_1(\mathcal{G})=\varnothing$. For the memoryless winning strategy $\sigma$, we fix an arbitrary total order on $V$ and choose $\sigma (v)=\text{min}\{v^{\prime }\in V\mid (v,v^{\prime })\in E\}$.

Case $k>0$: If $k$ is even, consider Player $i$, otherwise Player (1-$i$). Let $W_{i-1}$ be the set of positions where Player (1-$i$) has a memoryless winning strategy. We show that Player $i$ has a memoryless winning strategy $\sigma$ from $V\setminus W_{1-i}$ . Consider the subgame ${\mathcal{G}}^{\prime }$:

• $V_0^{\prime }=V_0\setminus W_{1-i},V_i^{\prime }=V_1\setminus W_{1-i},V^{\prime }=V_0^{\prime }\cup V_1^{\prime }$
• $E^{\prime }=E\cap (V^{\prime }\times V^{\prime })$
• $c^{\prime }(v)=c(v)\text{ for all }v\in V^{\prime }$

Note that ${\mathcal{G}}^{\prime }$ is still a game:

• for $v\in V_i^{\prime }$, there is a $v\in V\setminus W_{1-i}$ with $(v,v^{\prime })\in E^{\prime }$, otherwise $v$ would be in $W_{1-i}$
• for $v\in V_{1-i}^{\prime }$, for all $v^{\prime }\in V$ with $(v,v^{\prime })\in E^{\prime }$, $v^{\prime }\in V\setminus W_{1-i}$, hence there is a $v^{\prime }\in V^{\prime }$ with $(v,v^{\prime })\in E$.

Let $c^{\prime -1}(k)=\{v\in V^{\prime }\mid c^{\prime }(v)=k\}$ (set of highest color positions in $V^{\prime }$), and
Let $Y=Att{r}_i^{\prime }(c^{\prime -1}(k))$. (attractor here means the set of positions that at least visit $c^{\prime -1}(k)$ once)
Let ${\sigma }_A$ be the corresponding attractor strategy on ${\mathcal{G}}^{\prime }$ into $c^{\prime -1}(k)$, as defined in the proof of Theorem 11.1.

Now consider the subgame ${\mathcal{G}}^{″}$:

• $V_0^{″}=V_0^{\prime }\setminus Y,V_i^{″}=V_1^{\prime }\setminus Y,V^{″}=V_0^{″}\cup V_1^{″}$
• $E^{″}=E^{\prime }\cap (V^{″}\times V^{″})$
• $c^{″}:V^{″}\to \{0,\dots ,k-1\};c^{″}(v)=c^{\prime }(v)\text{ for all }v\in V^{″}$

Note that ${\mathcal{G}}^{″}$ is still a game, and that the maximal color in ${\mathcal{G}}^{″}$ is at most $k-1$ (we removed position that color as $k$ and positions that can visit it by Player $i$). By induction hypothesis, that ${\mathcal{G}}^{″}$ is memoryless determined.

It is also clear that $W_{1-i}^{″}$, the set of positions in game ${\mathcal{G}}^{″}$ where Player (1−$i$) has a memoryless winning strategy, is empty, because $W_{1-i}^{″}$ is a subset of $W_{1-i}$:

assume Player (1−$i$) had a memoryless winning strategy from some position in $V^{″}$. Then this strategy would win in $\mathcal{G}$, too, since Player $i$ has no opportunity to leave ${\mathcal{G}}^{″}$ other than to $W_{1-i}$.

Hence, there is a uniform winning memoryless winning strategy ${\sigma }_{IH}$ for player $i$ from all positions in $V^{″}$. We define the following uniform strategy $\sigma$ for Player $i$ in game $\mathcal{G}$:

$$\sigma (v)=\{\begin{array}{ll}{\sigma }_{IH}(v)& \text{if }v\in V^{″}\\ {\sigma }_A(v)& \text{if }v\in V\setminus c^{\prime -1}(k)\\ \text{min. successor in }V\setminus W_{1-i}& \text{if }v\in V\cap c^{\prime -1}(k)\\ \text{min. successor in }V& \text{otherwise.}\end{array}$$

The strategy $\sigma$ is winning for Player 0 on $V\setminus W_{1-\sigma }$. Consider a play that is consistent with $\sigma$, it can be either:

1. $Y$ (Set of positions that Player 0 can visit the highest color $k$) is visited infinitely often. Thus, Player $i$ wins.

2. Eventually only positions in $V^{″}$ are visited. Hence, since Player $i$ follows ${\sigma }_{IH}$, Player $i$ wins.

Construct $W_{1-i}$ with McNaughton’s algorithm

The proof above is non-constructive in the sense that we begin the argument by considering (rather than computing) the set $W_{1-i}$ of positions where the opponent, Player (1−$i$), has a memoryless winning strategy. McNaughton’s algorithm, one of the classic algorithms for parity games over finite arenas, computes this set iteratively, with repeated recursive calls:

$$\begin{gathered} \mathbf{\text{Construction 11.3. }}\text{Let a finite parity game }\mathcal{G}=(\mathcal{A},\text{PARITY}(C))\text{ be given. We compute the} \\ \text{winning regions }{W}_0(\mathcal{G})\text{ and }{W}_1(\mathcal{G})\text{ as follows. (To avoid confusion we indicate in each attractor} \\ \text{construction explicitly the game it refers to.)} \end{gathered}$$
$$\begin{gathered} \text{Function }\mathit{\text{McNaughton}}(\mathcal{G})= \\ \begin{array}{ll}1.& k:=\text{ highest color in }\mathcal{G}\\ 2.& \mathbf{\text{if }}k=0\text{ or }V=\varnothing \\ & \mathbf{\text{then return }}(V,\varnothing )\\ 3.& i:=k\text{ mod }2\\ 4.& W_{1-i}:=\varnothing \\ 5.& \mathbf{\text{repeat}}\\ & \begin{array}{ll}(a)& {\mathcal{G}}^{\prime }:=\mathcal{G}\setminus Att{r}^i(c^{-1}(k),\mathcal{G})\\ (b)& (W_0^{\prime },W_1^{\prime }):=\mathit{\text{McNaughton}}({\mathcal{G}}^{\prime })\\ (c)& \mathbf{\text{if }}(W_{1-i}^{\prime }=\varnothing )\mathbf{\text{ then}}\\ & \begin{array}{rl}\text{i.}& W_i:=V\setminus W_{1-i}\\ \text{ii.}& \mathbf{\text{return }}(W_0,W_1)\end{array}\\ (d)& W_{1-i}:=W_{1-i}\cup Att{r}^{1-i}(W_{1-i}^{\prime },\mathcal{G})\\ (e)& {\mathcal{G}}^{\prime }:=\mathcal{G}\setminus Att{r}^{1-i}(c^{-1}(W_{1-i}^{\prime },\mathcal{G})\end{array}\end{array} \end{gathered}$$

Explaination

(Line 1): The construction begins by determining the highest color $k$ that appears in the arena.

(Line 2): If this color is 0 (or the arena is empty), then Player 0 wins the game from all positions, function ends.

(Line 3): Otherwise we continue by analyzing the game from the perspective of Player $i=0$ if $k$ is even and from the perspective of Player $i=1$ if $k$ is odd.

(Line 4): We initialize the winning region for the opponent to $\varnothing$ and repeat the following:

(Line 5a): First, we eliminate all positions where Player $i$ can enforce a visit to the highest color $k$ (which, if visited infinitely often, is beneficial for Player $i$).

(Line 5b): We recursively solve the resulting subgame ${\mathcal{G}}^{\prime }$.

(line 5c): If the oppoent does not have any winning positions in the subgame, then we are done:

• If the play of $\mathcal{G}$ stays in the subgame, then Player $i$ wins with the winning strategy of the subgame.

• If the play leaves the subgame, then Player $i$ can enforce a visit to the highest color.

So either the play eventually stays in the subgame forever, and Player $i$ wins there, or it infinitely often leaves the subgame, and Player $i$ wins by visiting the highest color infinitely often.

(line 5d): If the opponent wins from some non-empty winning region $W_{1-i}^{\prime }$ of the subgame, then we add the opponent’s attractor of $W_{1-i}^{\prime }$ to the winning region of $\mathcal{G}$.

• The opponent is sure to win from every position in the attractor by first ensuring a visit to $W_{1-i}^{\prime }$ and then staying there forever applying its winning strategy inside ${\mathcal{G}}^{\prime }$.

• Player $i$ cannot force the game out of the subgame, because ${\mathcal{G}}^{\prime }$ was constructed by removing Player $i$’s attractor from $\mathcal{G}$.

(line 5e): We remove the entire attractor from $\mathcal{G}$ (line 5e) and continue with the resulting subgame.

Example

Consider again the example above.

(line 1): The highest color is $k=4$,
(line 3): k is even, hence $i=0$.
(line 5a): We have that $c^{-1}(4)=\{v_4,v_8\}$ and $Att{r}^0(c^{-1}(4))=Att{r}^0(\{v_4,v_8\})=\{v_3,v_4,v_6,v_7,v_8\}$. Hence, ${\mathcal{G}}^{\prime }$ is the subgame consisting of positions $v_0$, $v_1$, $v_2$, and $v_5$:

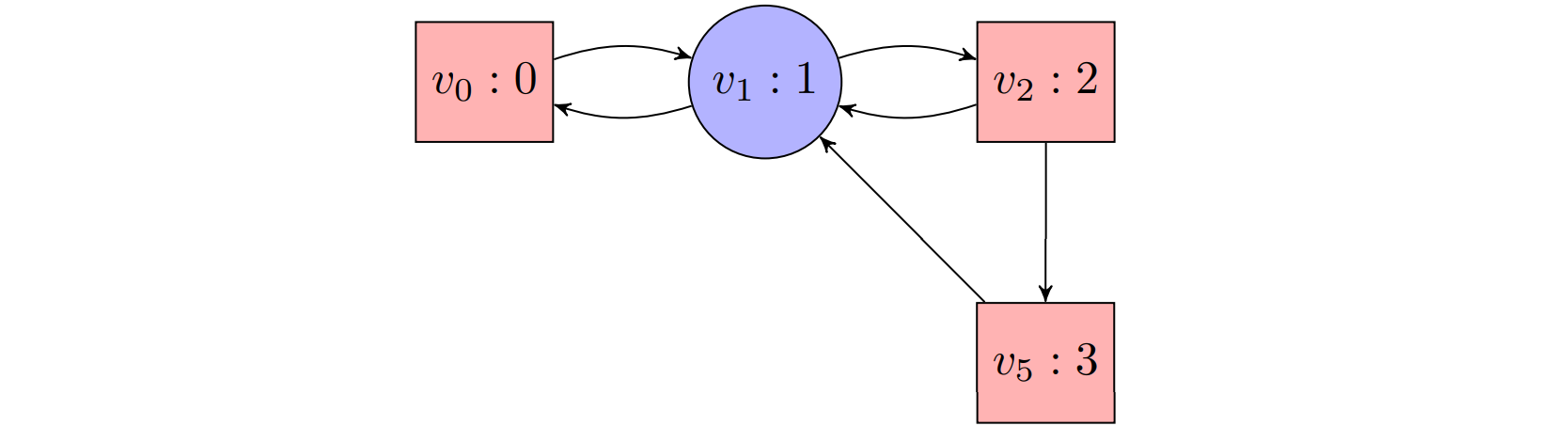
(line 5b): The recursive call returns $W_0^{\prime }=\varnothing ,W_1^{\prime }=\{v_0,v_1,v_2,v_5\}$. (We skip over the evaluation of the recursive call here, note that Player 1 wins from every position with a strategy that moves from $v_2$ to $v_5$.)
(line 5d): We have that $Att{r}^1(\{v_0,v_1,v_2,v_5\})=\{v_0,v_1,v_2,v_4,v_5,v_8\}$. Hence, $W_1$ is set to $\{v_0,v_1,v_2,v_4,v_5,v_8\}$,
(line 5e): And $\mathcal{G}$ is reduced to the subgame consisting of positions $v_3$, $v_6$ and $v_7$:

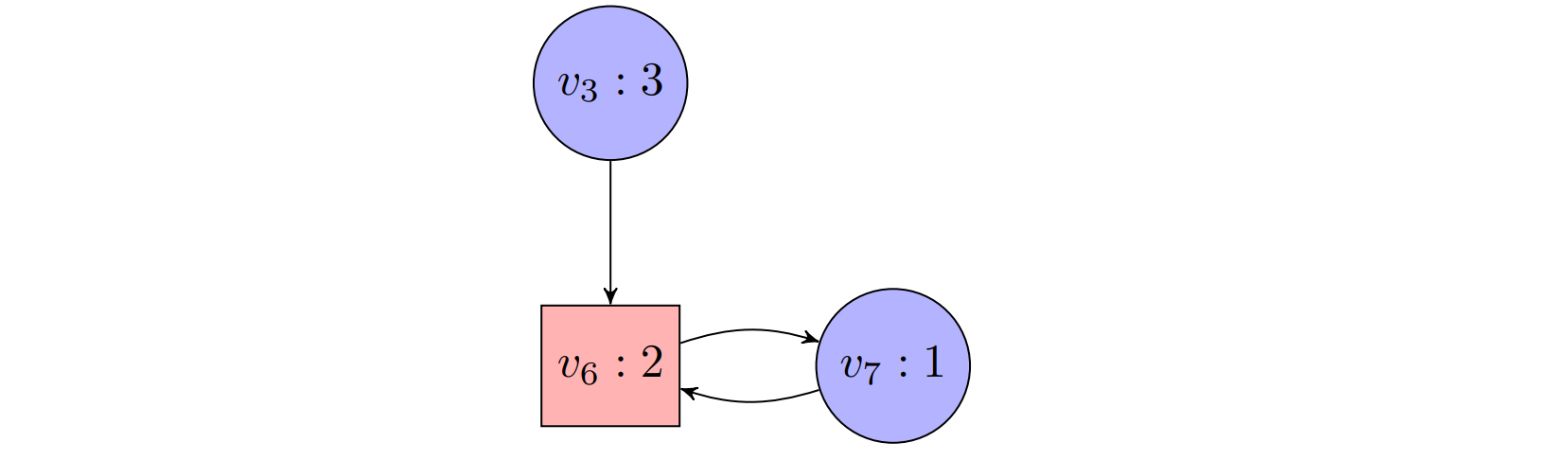
(line 5b): Now, the game does not contain any positions with color 4 anymore, we therefore call the algorithm recursively. It returns $W_0^{\prime }=\{v_3,v_6,v_7\},W_1^{\prime }=\varnothing$. (We again skip over the evaluation of the recursive call, note that all plays are winning for Player 0.)
(line 5ci): Since $W_1^{\prime }=\varnothing$, we set $W_0$ to $V\setminus W_1$,
(line 5cii): Return the final result $W_0=\{v_3,v_6,v_7\}$, $W_1=\{v_0,v_1,v_2,v_4,v_5,v_8\}$.

---

Next chapter: Muller Games

Further Reading: