AGV -- (Exercise 7.2) LTL to Alternating Büchi Automata

Previous Exercise:

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

This is an example exercise to express LTL formula into Alternating Büchi Automata. For further definitions, you may check Section 7.2.

Question

Use the construction from the lecture to construct an alternating Büchi automaton $\mathcal{A}$ such that $$\mathcal{L(A)=L}((\Diamond p)\ \mathcal{U}\ (\square q))$$

Solution

we build the following alternating Büchi automaton $\mathcal{A} = (2^{p,q},Q,\varphi,\delta,\small\text{BÜCHI} \normalsize(F))$ which recognizes the models of $\varphi=(\Diamond p)\ \mathcal{U}\ (\square q)$. First we consider the transition function $\delta$ for an arbitrary symbol $a\in2^{p,q}:$

$\begin{array}{lll}
\hspace{1cm}\bullet &&\delta(\square q,a)\newline
&=&\delta(\neg(\textit{true}\ \mathcal{U}\ \neg q) ,a)\newline
&=&\overline{\delta(\textit{true}\ \mathcal{U}\ \neg q ,a)}\newline
&=&\overline{\delta(\neg q,a)\vee(\delta(\textit{true},a)\wedge(\textit{true}\ \mathcal{U}\ \neg q))}\newline
&=&\overline{\delta(\neg q,a)}\wedge\overline{(\delta(\textit{true},a)\wedge (\textit{true}\ \mathcal{U}\ \neg q))}&(\textit{true}\wedge \psi=\psi)\newline
&=&\overline{\delta(\neg q,a)}\wedge\overline{(\textit{true}\ \mathcal{U}\ \neg q)}&(\text{Using line 1})\newline
&=&\overline{\delta(\neg q,a)}\wedge\square q\newline
&=&\left\lbrace \begin{array}{lll}
\square q&\text{if }q\in a\newline
\textit{false}&\text{if }q\notin a\newline
\end{array}\right.
\end{array}
\ \newline \ \newline
\begin{array}{lll}
\hspace{1cm}\bullet &&\delta(\Diamond p,a)\newline
&=&\delta(\textit{true}\ \mathcal{U}\ p ,a)\newline
&=&\delta(p,a)\vee(\delta(\textit{true},a)\wedge\Diamond p)&(\textit{true}\wedge \psi=\psi)\newline
&=&\delta(p,a)\vee\Diamond p\newline
&=&\left\lbrace \begin{array}{lll}
\Diamond p&\text{if }p\notin a\newline
\textit{true}&\text{if }p\in a\newline
\end{array}\right.
\end{array}
$

By Substitution above result into $\delta((\Diamond p)\ \mathcal{U}\ (\square q),a)=\delta(\square q,a)\vee(\delta(\Diamond p,a)\wedge(\Diamond p)\ \mathcal{U}\ (\square q))$, we have:

$$\delta((\Diamond p)\ \mathcal{U}\ (\square q),a)=\left\lbrace
\begin{array}{lll}
\Diamond p\wedge((\Diamond p)\ \mathcal{U}\ (\square q))&\text{if }a =\varnothing &(\vee\ \textit{false}\text{ is omitted.})\newline
(\Diamond p)\ \mathcal{U}\ (\square q)&\text{if }a =\lbrace p\rbrace&(\wedge\ \textit{true}\text{ is omitted.})\newline
\square q\vee(\Diamond p\wedge((\Diamond p)\ \mathcal{U}\ (\square q)))&\text{if }a =\lbrace q\rbrace\newline
\square q\vee((\Diamond p)\ \mathcal{U}\ (\square q))&\text{if }a =\lbrace p,q\rbrace&(\wedge\ \textit{true}\text{ is omitted.})\newline
\end{array}\right.$$

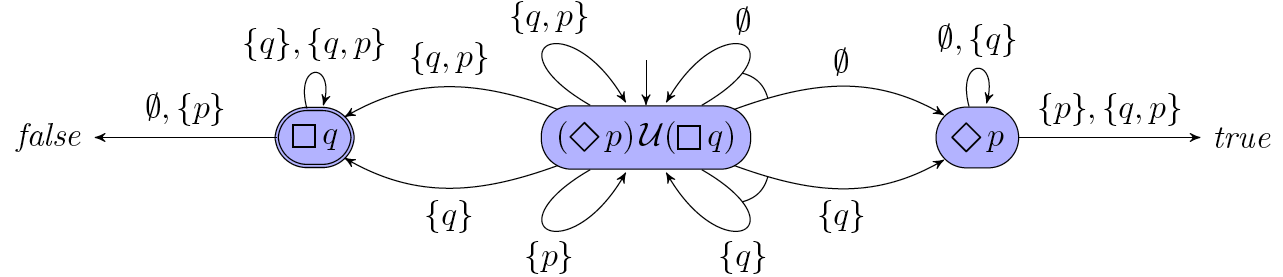
For each case, when we see $\vee$, that’s a nondeterministic transitions, we need draw two seperate transitions for each successors. On the other hand $\wedge$ is a universal transitions, it is a single transition towards both successors, we split the extra branches from the path to indicate that. Thus we have the following automaton $\mathcal{A}$:

---

Next Exercise:

Further Reading: