AGV 9.2 -- Nested depth-first search

Previous chapter: Automata-based LTL Model Checking with Sequential Circuits

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

We now develop an algorithm for checking whether the language of a given Büchi automaton is empty. A natural idea is to use depth-first search (DFS) twice.

The language is non-empty $\Leftrightarrow$ it is accepted by some words:

1. there exists an accepting state $q$,
2. $q$ is reachable from some initial state (discovered by 1st DFS), and
3. $q$ can again be reached from $q$ (discovered by 2nd DFS),

Example (Simple DFS)

Consider the following Büchi automaton (edge labels do not matter and are omitted).

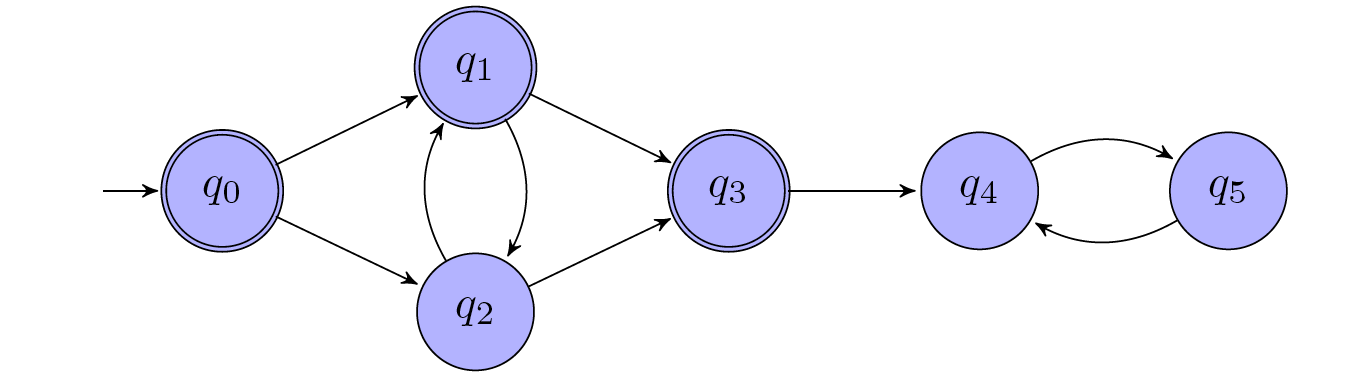
Step 1: discovers $q_0$, $q_1$, and $q_3$.
Step 2: searches from $q_0$ and $q_3$: not successful; searches from $q_1$: discovers the path back to $q_1$ via $q_2$.

The drawback of the algorithm discussed so far is its quadratic running time: potentially, each state in $F$ discovered by the first DFS requires a fresh second DFS. The quadratic running time can be avoided by stopping the DFS in Step 2 whenever a state is encountered that was already visited during Step 2.

However, this is only sound if the searches in Step 2 are executed in the right order. If we first execute the DFS from $q_0$ in Example 9.2, then this search visits all states; in a subsequent search from $q_1$, we would, therefore, no longer discover the successful path back to $q_1$ via $q_2$!

It turns out that it is sound to restrict the searches in Step 2 if they are executed in order of increasing finishing times of the DFS in Step 1. The emptiness check with nested DFS therefore uses Step 1 to order the reachable accepting states according to their finishing times; in Step 2, a DFS is initiated from each reachable accepting state in this order until a cycle is detected. Step 2 marks the visited states and restricts the searches so that no state is visited twice during Step 2.

A Modified Example (Nested DFS)

Continue from above, a possible annotation of the states with pairs (discovery, finishing) of discovery and finishing times during the DFS in Step 1 is the following:

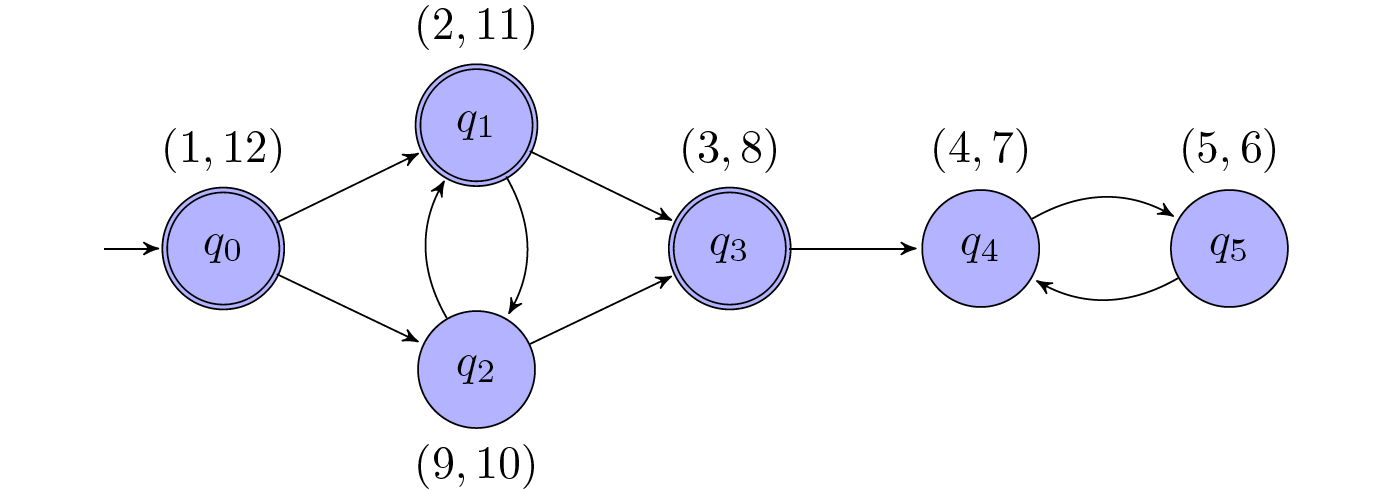
Ordering the accepting states according to increasing finishing times, we obtain the order $q_3$, $q_1$, $q_0$. In Step 2, the DFS from $q_3$ visits (unsuccessfully) $q_3$, $q_4$ and $q_5$. The DFS from $q_1$
then only visits $q_1$ and $q_2$, upon which it has successfully discovered the path from $q_2$ to $q_2$.

Nested DFS and Büchi Automaton

$\textbf{Theorem 9.1. }\textit{For a Büchi automaton }\mathcal{A}\textit{, nested DFS is successful iff }\mathcal{L(A)}\textit{ is nonempty.}$

Proof

$”\Rightarrow”$
If the nested DFS is successful then there exists a state $q$ that is reachable from some initial state such that there is a path from $q$ back to $q$. Hence, $\mathcal{L(A)}$ is non-empty.

$”\Leftarrow”$
To show that we can safely ignore the states that were visited in previous searches in Step 2, we consider the situation at the beginning of a DFS from some accepting state $q\in F$ in Step 2. Let $T$ be the set of states visited in previous searches in Step 2. We prove that there is no cycle $q_0,q_1,\dots,q_k$ with $q=q_0=q_k$ such that $\lbrace q_0,q_1,\dots,q_k\rbrace\cap T\neq \varnothing$ i.e., the states in $T$ can be ignored while looking for $q$-cycles.

Assume, by way of contradiction, that there is a state $q$ where this condition is violated for the first time. Let $t\in\lbrace q_0,q_1,\dots,q_k\rbrace\cap T$, and let $u\in F$ be the accepting state such that $t$ has been added to $T$ during the DFS in Step 2. This means that the DFS from $u$ was invoked before the DFS from $q$; hence, $u$ has an earlier finishing time than $q$ in den DFS of Step 1.

• Case 1: $u$ was discovered before $q$ in the DFS of Step 1. This cannot be the case, because $q$ is reachable from $u$, and, thus, the finishing time of $q$ would have been earlier than that of $u$.

• Case 2: u was discovered after $q$ in the DFS of Step 1. Then $q$ was still on the stack of the DFS when $u$ was finished. Hence, $u$ is reachable from $q$. Thus, $u$ and $q$ are on a cycle. This cycle (or some other cycle) would have been discovered during the DFS from $u$ in Step 2.

---

Next chapter: The Emerson-Lei algorithm

Further Reading: