Crpytography 1 -- Historical Ciphers & Cryptanalysis

This is a learning note of a course in CISPA, UdS. Taught by Nico Döttling

Substitution Ciphers (∼?)

• One of the oldest cipher in the world, used in the bible (Atbash)
• Reorder the alphabet list to create a substitution list
• Number of keys: $26!$

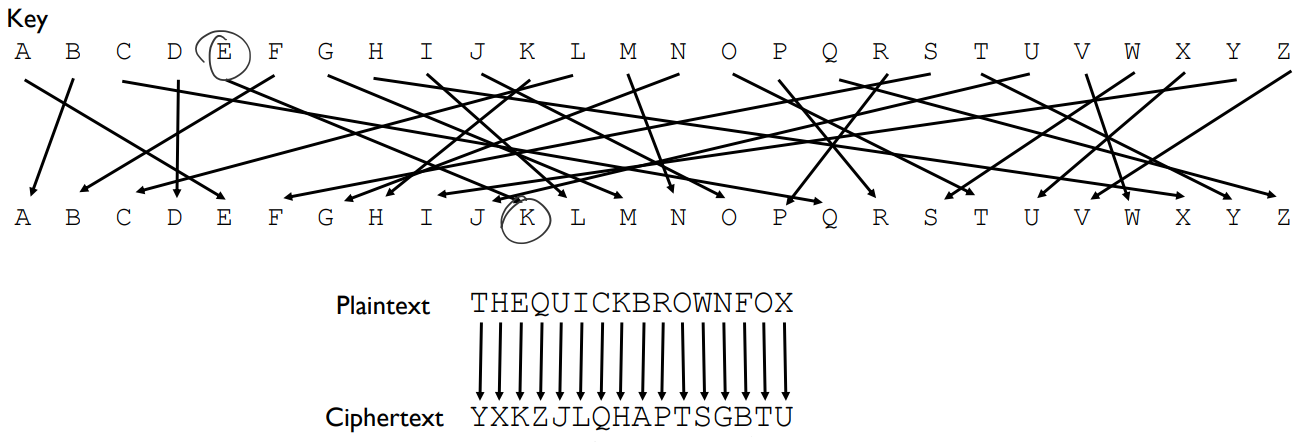
Shift Cipher

• Create the substitution list by shifting the alphabets
  • Each letter in the plaintext is replaced by a letter some fixed number (key) of positions down the alphabet.
• Number of keys: $26$

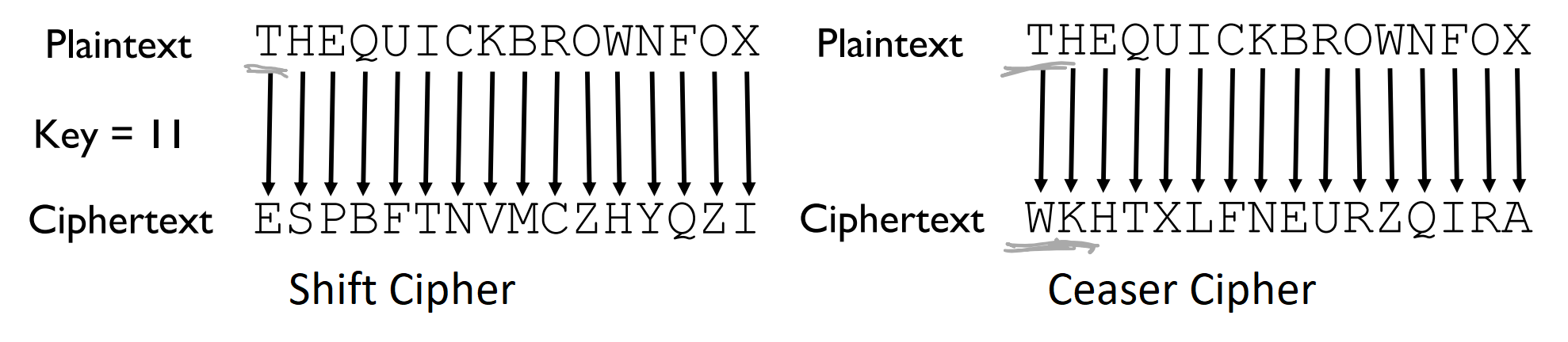
Caesar Cipher (∼70 BCE)

• A speical form of shift cipher
  • shift left by exactly 3 (key = 3)

The Vigenère Cipher (∼1500)

• Variant of Shift Cipher, called Polyalphabetic cipher
  • Every character (can) shift independently
  • Different character can be encrypted as same character
• Usually only use a repeating word/phrase as a key instead of encrypt every character one by one
  • First create a word, e.g. MOTH
  • Shift
• Number of keys: $26^{n}$

---

Cryptanalysis of the Vigenère Cipher

• Cryptanalysis is the science of breaking codes and deciphering encrypted messages without knowing the key or the encryption algorithm
  • Can we guess the key/plaintext by investigating the Ciphertext?

Known knowledge of Vigenère Cipher

• Vigenère Cipher is a shift cipher with substrings (key)
• Key length is a secret
  • Need to first guess the key length before guessing the key itself

Kasiski examination

• Find the duplicate phrase/strings that appeared in the ciphertext
• Calculate the distance between two phrase to deduce the key length

• In the example, the distance between the two V in VHVS is 18, and the distance is 30 for Q in QUCE
• The common factors of 18 and 30 are 1, 2, 3, 6
• We can guess the key length as 6, since 1, 2, 3 may be too short for a key

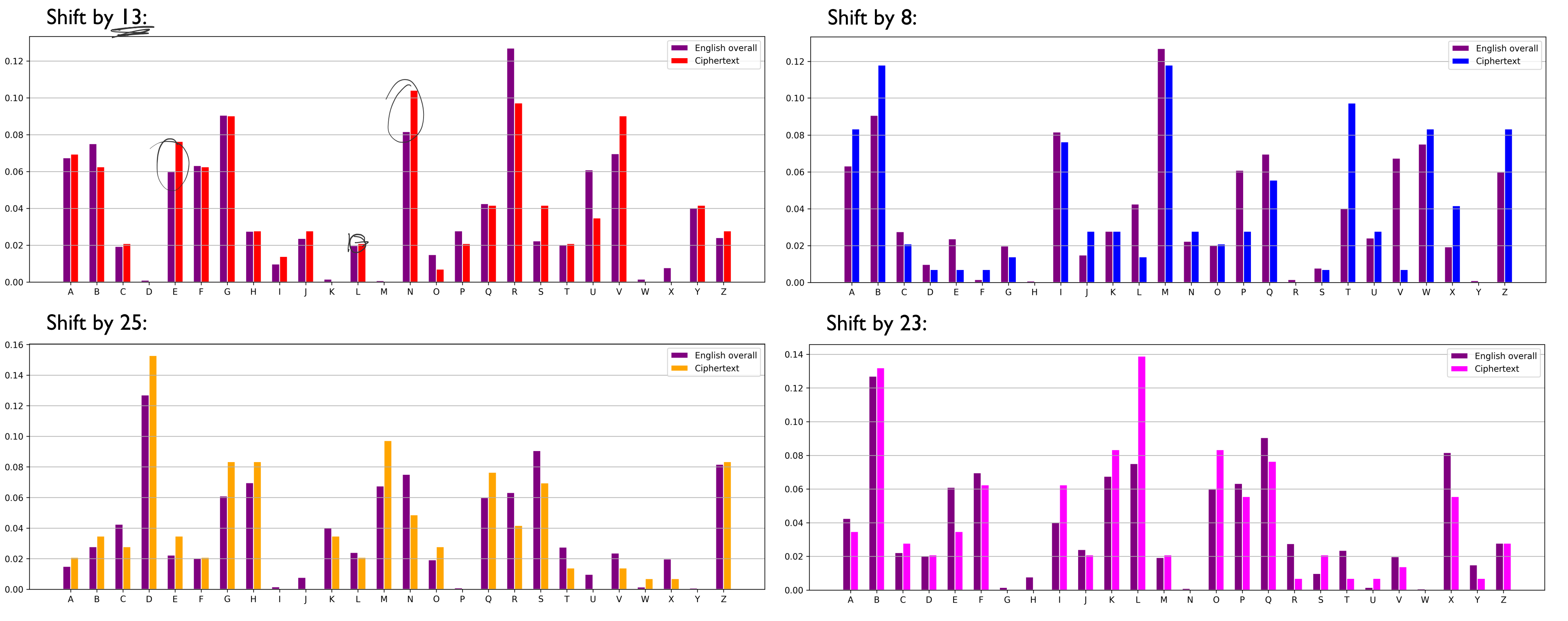
Frequency Analysis

• Every langauge has a pattern/frequency of the characters used
• A short piece of text (should) show a similar distribution as the language as a whole
• We can split the text based on the key length we are guessing
  • e.g. 12341234… $\Rightarrow$ 111…222…333…444..
• Now each set of letters are simple shift cipher
  • apply frequency test by shifting them step by step
  • if they show similar frequency pattern, there is a high chance that it is the correct encrpytion (Friedman test)

---

Cryptanalysis of the Substitution Cipher

• Using Frequency Analysis on alphabet, we can only those who have highest/lowest frequency
  • Natural language also has frequent character constellations
  • Generalize character frequencies: Bigrams, trigrams, …N-grams

• Plaintext recovery requires a lot of context information and guessing
  • strongest possible attack
  • Language? Context?

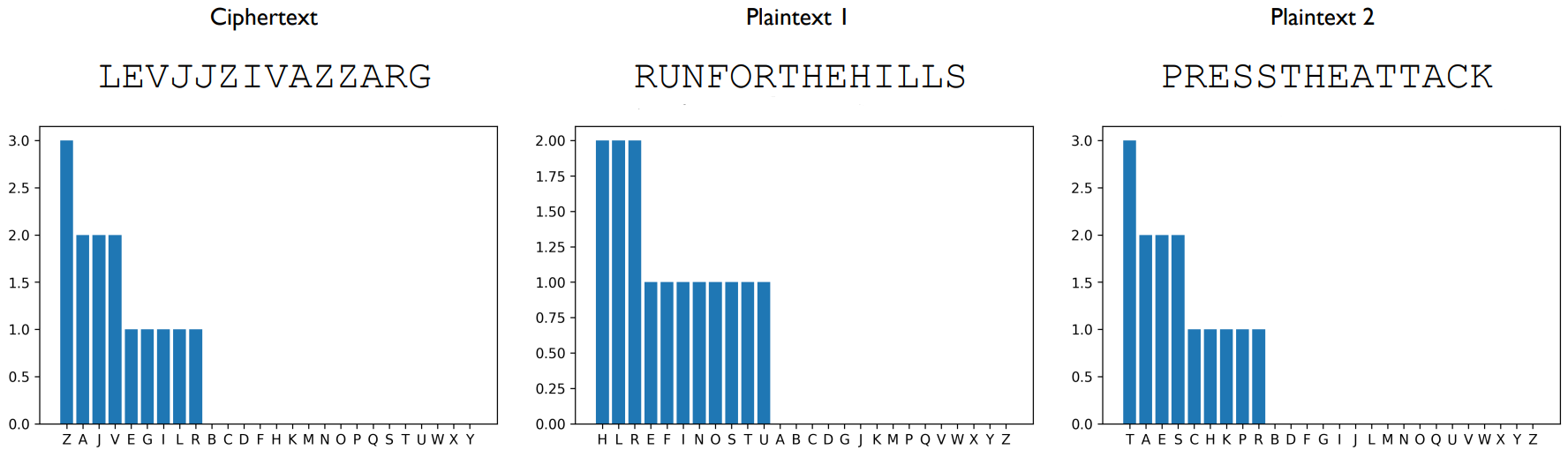
Extreme Case: 1 Ciphertext, 2 Plaintexts

• Guess which plaintext is encrypted into the ciphertext
• Structural Property of Cipher: Same letters always encrypt to same letter

---

Some Lessons from Historic Ciphers

• Ciphers without keys or small key-space cannot recover from compromise
• Ciphertext should not reveal statistical information about plaintexts
• Further thoughts: Many historic ciphers immediately broken given a single message-ciphertext pair

---

Kerkhoff’s Principle

The cipher method must not be required to be secret, and it must be able to fall into the hands of the enemy without inconvenience.

• Designs which violate Kerkhoff’s principle = achieve Security by Obscurity
  • Nowadays obscurity is considered bad cryptographic design
• It is easier to switch a compromised key than a compromised design

---

Next post: Probability Theory

Further Reading: History of cryptography