Parameterized Verification 1.2 -- Synchronization Primitives of Processes

This is a learning note of a course in CISPA, UdS. Taught by Swen Jacobs

Last post: Labeled Transition Systems

Processes

A Process is an LTS $P = (Q, Q_0, \Sigma, \delta, \lambda)$ with $\Sigma = \Sigma_{int} \cup \lbrace out_a , in_a \mid a \in \Sigma_{sync} \rbrace $, where

• $\Sigma_{int}$ is a set of internal actions,
• $\Sigma_{sync}$ a set of synchronizing actions,
• $out_a$ is an send action (or initiate action),
• $in_a$ is an receive action.

Composition by Synchronization

The composition $P^n$ of $n$ (uniform) processes wrt. $card$ is the LTS $(S, S_0, \Sigma_{int} \cup \Sigma_{sync}, \Delta, \Lambda)$ with:

• $S = Q \times Q$

• $S_0 = Q_0 \times Q_0$

• $\Delta \subseteq S \times (\Delta_{int} \cup \Delta_{sync} \times S)$ is the set of all transitions that satisfy one of the following:

  Internal Transition:

  • For some $i \in\lbrace 1, … , n \rbrace$ , $(s, a, s’) \in S \times\Sigma_{int}\times S$ is an element such that:
    $(s(i), a, s’(i)) \in\delta$ , and $s(j) = s’(j)$ for $i \ne j \in\lbrace 1, …, n \rbrace$

  Process $s(i)$ take the action, other processes $s(j)$ remain their current states.

  Synchronous Transition

  • For some $i \in \lbrace 1, … , n \rbrace$ and some $I \subseteq \lbrace 1, …, n \rbrace \setminus \lbrace i \rbrace$ with $|I| \in card$ ,
    $(s, a, s’) \in S \times \Sigma_{int} \times S$ is an element such that:

    • $s(i) \buildrel out_a \over\longrightarrow s’(i)$ is (a local transition) in $P$

      One process $s(i)$ take the send action.

    • for every $j \in I, s(j) \buildrel in_a \over\longrightarrow s’(j)$ is (a local transition) in $P$

      $I$ is the set of processes that can take the receive action. (size of $I$ must not be larger then $card$)

    • for every $j \in\lbrace 1, …, n \rbrace \setminus (I \cup\lbrace i \rbrace), s’(j) = s(j)$

      Other processes $s(j)$ that cannot take receive actions remain their current states.

    • $I$ is maximal.

      There does not exist a larger set $I’ \supset I$ with $|I’| \in card$ that for all $j \in I’$ ,
      there is a local transition from $s(j)$ that can take the receive action.

• $\Lambda(s) = \lbrace p_{i} \mid p \in \text{AP and p} \in\lambda(s(i)), i \in \lbrace 1, …, n\rbrace \rbrace$

In this course, send action = $out_a$ = $a!!$ ; receive action = $in_a$ = $a??$.

Example of Composition by Broadcast synchronization. $(card = \lbrace 1 \rbrace)$

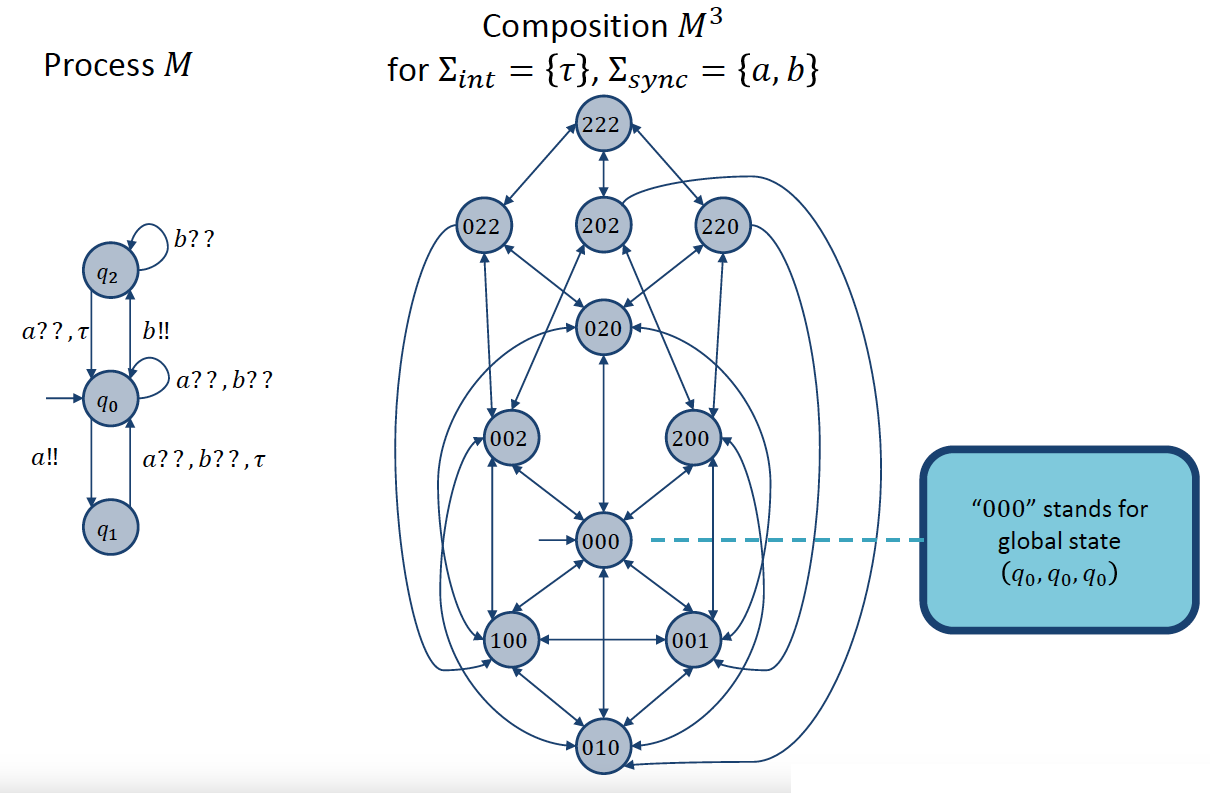
Synchronization Primitives

In this course, there are 4 types of synchronization:
Pairwise Rendezvous, Broadcast, Asynchronous Rendezvous, and Lossy Broadcast.

Pairwise Rendezvous

Exactly ONE process take $out_a$ action, ONE process take $in_a$ action. $(card = \lbrace 1 \rbrace)$

Broadcast

ONE process take $out_a$ action, ALL process take $in_a$ action if they are able to $(card = \mathbb{N}_0)$.

Asynchronous Rendezvous

ONE process take $out_a$ action, ZERO / ONE process take $in_a$ action $(card = {0, 1})$.

Lossy Broadcast

ONE process take $out_a$ action, ONE process take $in_a$ action $(card = \mathbb{N}_0, I\text{ not necessarily maximal})$.

---

Next post:

Further Reading: Synchronization, Parameterized Verification by Javier Esparza.