AGV 11.2 -- Reachability Games
Previous chapter: Infinite Games (Basic Definitions)
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Reachability Condition
We will now analyze infinite games for various types of winning conditions. We start with the simple reachability condition.
The reachability condition is given as a set $R$ of positions called the reachability set. The reachability condition is satisfied if the play reaches some position in $R$. Formally, for an infinite word $\alpha$ over $\Sigma$, we use $\text{Occ}(\alpha) := \lbrace\sigma\in\Sigma\mid\exists n\in\mathbb{N}.\ \alpha(n)=\sigma\rbrace$ to denote the set of all letters occurring in $\alpha$.
$\textbf{Definition 11.11. } \text{The }\textit{reachability condition }\small\text{REACH} \normalsize(R)\text{ on a set of positions }R\subseteq V\text{ is the set}$
$$ \small\text{REACH} \normalsize(R) = \lbrace\rho\in V^\omega\mid\text{Occ}(\rho)\cap R\neq\varnothing\rbrace$$
$$\text{A game }\mathcal{G}=(\mathcal{A},\text{Win})\text{ with Win}=\small\text{REACH} \normalsize(R)\text{ is called a }\textit{reachability game}\text{ with reachability set }R $$
Example
$$
\text{Position of Player 0: Circles;}\ \ \text{Positions of Player 1: rectangles.}$$
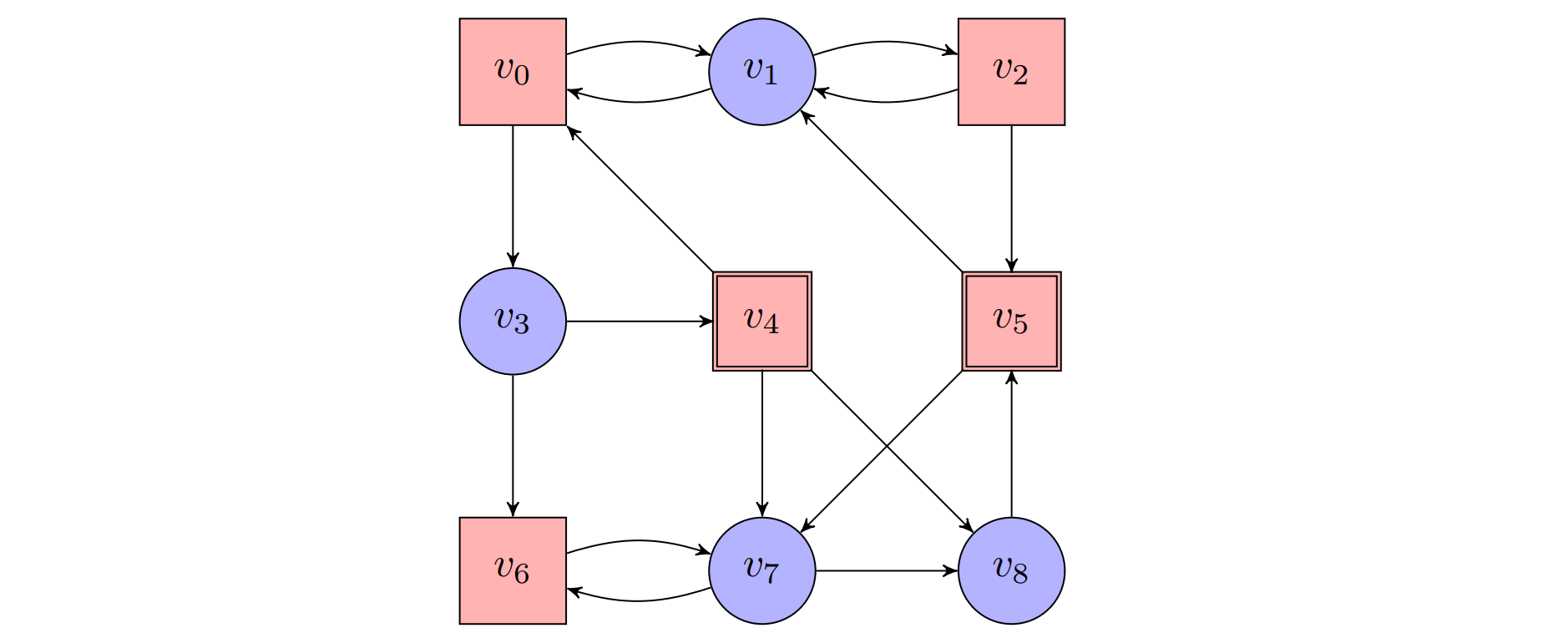
$$\mathcal{G}=(\mathcal{A},\small\text{REACH} \normalsize(R)),\ R=\lbrace v_4,v_5\rbrace
$$