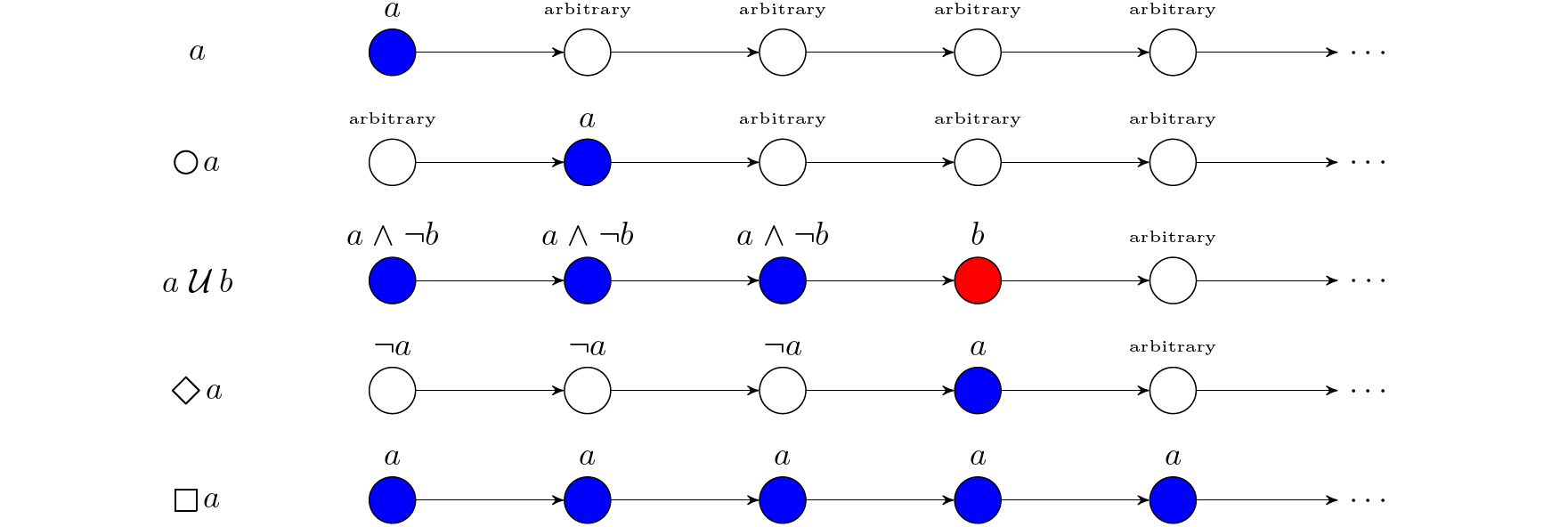
AGV 6.7 -- S1S$_0$ and Büchi-recognizable Language
Previous chapter: Express QPTL using S1S
This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner
Introduction
To prepare for the proof that every S1S-definable language is Büchi-recognizable, we show in the following lemma that we can focus on a restricted sublogic, called S1S$_0$, which is defined by the following grammar:
$$\varphi::=0\in X\mid x\in Y\mid x=0\mid x=y\mid x=S(y)\mid \neg\varphi\mid\varphi\wedge\varphi\mid\exists x.\varphi\mid\exists X.\varphi$$
- Membership tests $(\in)$: variables $(x,y,\dots)$ and $0$ only
- Equalities $(=)$: variables $(x,y,\dots)$, $0$ and a single successor operation $(S(t))$ only
- i.e. $S(S(t))$ is not allowed.
Complex formula in S1S can then be simplified by introducing additional variables.
From S1S to S1S$_0$
$\textbf{Lemma 6.1. } \textit{For every S1S formula }\varphi\textit{ there is an S1S}_0\text{ formula }\varphi’\textit{ such that }\mathcal{L}(\varphi)=\mathcal{L}(\varphi’).$