Parameterized Verification 1.1 -- Labeled Transition Systems

This is a learning note of a course in CISPA, UdS. Taught by Swen Jacobs

Labeled Transition Systems (LTS)

LTS is a concept in theoretical computer science used in the study of computation. It is used to describe the potential behavior of discrete systems, e.g. Model Checking.

It consists of states and transitions between states, which may be labeled with labels chosen from a set; the same label may appear on more than one transition. Mathematically, it can be described as directed graph.

Labels

Labels can be used to describe the behaviour or distinguish between states.
If the set of label is a singleton (only contains one label), then it can be omitted in the system.

LTS v.s. Finite-state Automata

In Transition systems:

• The set of states is not necessarily finite, or even countable.
• The set of transitions is not necessarily finite, or even countable.
• No “start” state or “final” states are given.

Formal definition

Let $AP$ be a set of atomic propositions (statement or assertion that must be true or false),
i.e., observable properties of the system.

A labeled transition system (LTS) over $AP$ is a tuple $Q, Q_0, \Sigma, \delta, \lambda$, where

• $Q$ is a set of states
• $Q_0 \subseteq Q$ is the set of initial states
• $\Sigma$ is the set of transition labels (or actions)
• $\delta \subseteq Q \times \Sigma \times Q$ is the transition relation (also write as $ q\buildrel a \over\rightarrow q’ \in \delta$)
• $\lambda : Q \rightarrow 2^{AP}$ is the state labeling.

In this course, we assume finite LTS, which means $AP$ and $Q$ are finite, unless explicitly stated.

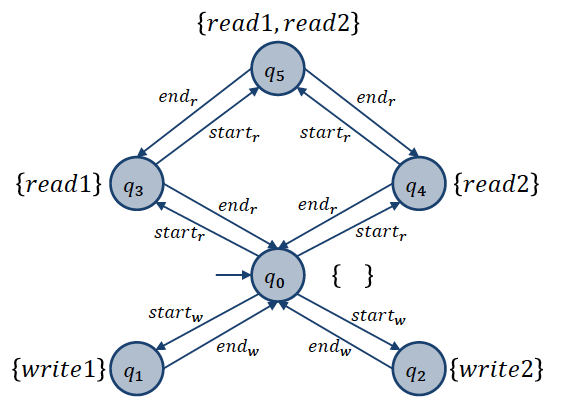
Run of an LTS

Consider an LTS $M = (Q, Q_0, \Sigma, \delta, \lambda)$.

Path

A path of $M$ an is a finite sequence $q_0a_0q_1a_1…q_n \in (Q\Sigma)\ast Q$, such that $ q_i \buildrel a_i \over\rightarrow q_{i+1}$ for all $i < n$
or an infinite sequence $q_0a_0q_1a_1…q_n \in (Q\Sigma)^\omega$, such that $ q_i \buildrel a_i \over\rightarrow q_{i+1}$ for all $i \in \mathbb{N}$.

Run

A run of $M$ is a path of $M$ with $q_0 \in Q_0$, and that is maximal, i.e., it cannot be extended.

A run is deadlocked if it is finite.

State-labeled paths

$q_0q_1…$, the projection of a path onto states $Q$,

Action-labeled paths

$a_0a_1…$, the projection of a path onto actions $\Sigma$,

Traces

$\lambda (q_0)\lambda q_1…$, the sequence of labels of a state-labeled path.

---

Next post: Synchronization Primitives of Processes

Further Reading: Transition System, Model Checking.