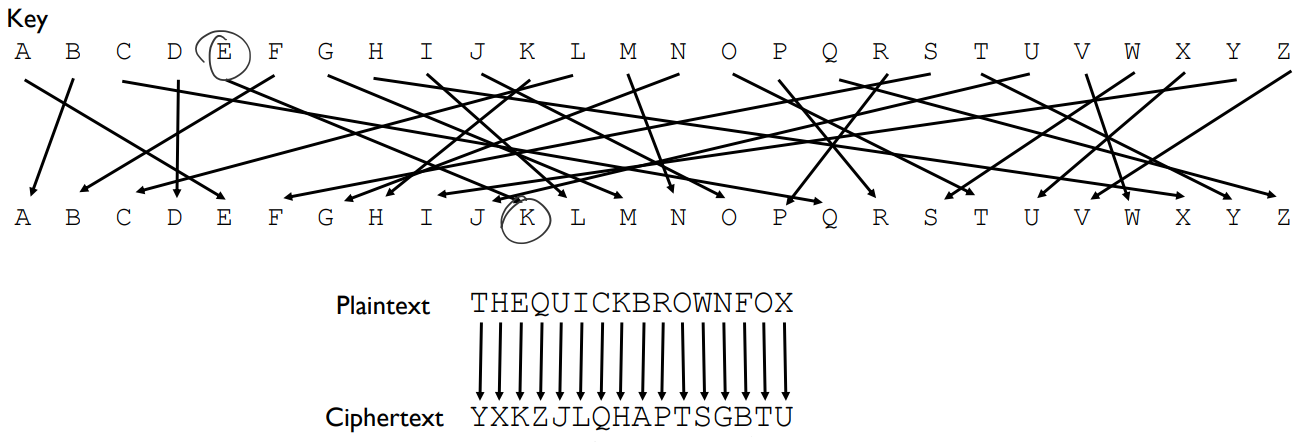
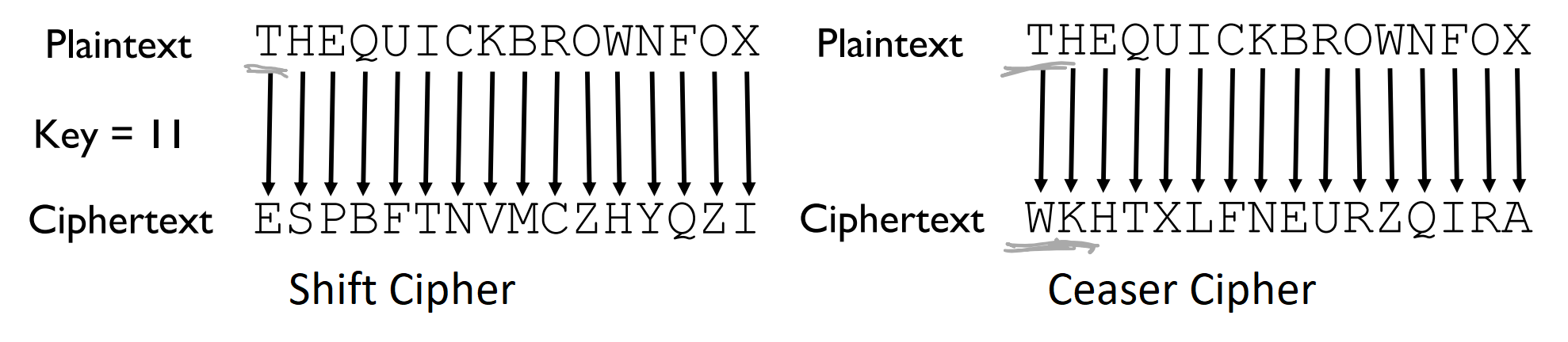
Previous chapter: Historical Ciphers & Cryptanalysis

This is a learning note of a course in CISPA, UdS. Taught by Nico Döttling

This chapter is a basic probability concept recap and clarify the syntax when writing them, useful if your memory start fading. Remember,

$$\textbf{Cryptography is impossible without randomness!}$$

Probability Spaces

Components	Definition	Remarks
$\Omega$	Sample Space	A finite set
$\omega\in\Omega$	Elementary Events / Outcomes
$Pr:\omega\rightarrow\mathbb{R}$	Probability Function	$\forall\omega\in\Omega. 0\leq Pr[\omega]\leq1, \underset{\omega\in\Omega}{\sum}Pr[\omega] = 1$
$E\subseteq\Omega$	Event	$\Pr[E] = \underset{\omega\in\Omega}{\sum}Pr[\omega], \text{ where } Pr[\varepsilon] = 0$

Examples

• Fair coin: $\Omega = {0,1}, Pr[0]=Pr[1]=1/2$
• Biased coin: $\Omega = {0,1}, Pr[1]=p, Pr[0]=1-p$
• Fair dice: $\Omega = {1,2,3,4,5,6}, Pr[1]=Pr[2]=\dots=Pr[6]=1/6$
• Uniform Randomness: $\Omega = {1.\dots,N}, Pr[1]=Pr[2]=\dots=Pr[N]=1/N$

Set Operations on events

Operations	Definition
$Pr[E_1\cap E_2] := Pr[E_1\wedge E_2] := Pr[E_1 \textbf{ AND } E_2] := Pr[E_1, E_2]$	Intersection, Logical ‘AND’
$Pr[E_1\cup E_2] := Pr[E_1\vee E_2] := Pr[E_1 \textbf{ OR } E_2]$	Intersection, Logical ‘OR’
$Pr[\overline{E}] := Pr[\neg E] := Pr[\textbf{NOT }E] \text{ where }\overline{E}=\Omega\setminus E$	Complement, Logical ‘Negation’
$A\subseteq B$, $A\Rightarrow B$	The event A implies the event B

This is a learning note of a course in CISPA, UdS. Taught by Nico Döttling

Substitution Ciphers (∼?)

• One of the oldest cipher in the world, used in the bible (Atbash)
• Reorder the alphabet list to create a substitution list
• Number of keys: $26!$

Shift Cipher

• Create the substitution list by shifting the alphabets
  • Each letter in the plaintext is replaced by a letter some fixed number (key) of positions down the alphabet.
• Number of keys: $26$

Caesar Cipher (∼70 BCE)

• A speical form of shift cipher
  • shift left by exactly 3 (key = 3)

The Vigenère Cipher (∼1500)

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Chapter 1. Introduction

Sections	Exercise
1.1. Model Checking
1.2. Synthesis
1.3. The Logic-Automata Connection

Chapter 2. Büchi Automata

Sections	Exercise
2.1. Preliminaries
2.2. Automata over Infinite Words
2.3. The Büchi Acceptance Condition

Chapter 3. Büchi’s Characterization Theorem

Sections	Exercise
3.1. Kleene’s Theorem
3.2. $\omega$-regular language
3.3 Closure Properties of the Büchi-recognizable languages (Intersection and Union)
3.4 Closure Properties of the Büchi-recognizable languages (Concatenations)
3.5 Büchi’s Characterization Theorem

Chapter 4. Deterministic Büchi Automata

Sections	Exercise
4.1. Deterministic vs. Nondeterministic Büchi Automata
4.2. Complementation of deterministic Büchi Automata

Chapter 5. Complementation of Büchi automata

Previous chapter: Emptiness Game

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

We now prove that parity tree automata are closed under complementation. As discussed at the beginning of the section, our proof makes heavy use of the determinacy of parity games (with infinite game arenas) established in Theorem 11.3.

$\textbf{Theorem 12.3. } \textit{For every parity tree automaton }\mathcal{A}\textit{ over }\Sigma\textit{ there is a parity tree automaton }\mathcal{A}’$ $\textit{ with }\mathcal{L(A’)}=\mathcal{T}_\Sigma\setminus\mathcal{L(A)}.$

Proof

Let $\mathcal{A}=(\Sigma,Q,q_0,T,\small\text{PARITY} \normalsize(C))$. By Theorem 12.1, a tree $(\mathcal{T},t)$ is accepted by $\mathcal{A}$ iff Player 0 has a winning strategy from position $(\varepsilon,q_0)$ of the acceptance game $\mathcal{G}_{\mathcal{A},t}$.

Since $\mathcal{A}$ is a parity tree automaton, $\mathcal{G}{\mathcal{A},t}$ is a parity game and therefore, by Theorem 11.3, memoryless determined. Hence, $\mathcal{A}$ does not accept some tree $t$ iff Player 1 has a winning memoryless strategy $\sigma$ in $\mathcal{G}{\mathcal{A},t}$ from $(\varepsilon,q_0)$.

The strategy $\sigma:\lbrace 0,1\rbrace^\ast\times T\rightarrow\lbrace 0,1\rbrace^\ast\times Q$ can be represented as a function $\sigma’:\lbrace 0,1\rbrace^\ast\times T\rightarrow\lbrace 0,1\rbrace$

where $\sigma(w,(q,\sigma,q^0,q^1))=(wi,q^i)$ iff $\sigma’(w,(q,\sigma,q^0,q^1))=i$. Yet another representation of the same strategy is $\sigma’:\lbrace 0,1\rbrace^\ast\rightarrow\lbrace T\rightarrow\lbrace 0,1\rbrace\rbrace$,

Previous chapter: Tree Automata and Acceptance Game

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Emptiness Game

The acceptance game can also be used to test if the language of a given tree automaton is non-empty. For this purpose, we first translate the given automaton into an automaton with singleton alphabet.

$\textbf{Construction 12.1. } \text{For a given tree automaton }\mathcal{A}\text{ over }\Sigma\text{-labeled trees, we consider the}$ $\text{following tree automaton }\mathcal{A}’\text{ over }\lbrace1\rbrace\text{-labeled trees, such that }\mathcal{L(A)}=\varnothing\text{ iff }\mathcal{L(A’)}=\varnothing:$

$\begin{array}{l}
\hspace{1cm} \cdot \ Q’=Q \newline
\hspace{1cm} \cdot \ q_0’=q_0\newline
\hspace{1cm} \cdot \ T’=\lbrace(q,1,q’,q’’)\mid(q,\sigma,q’,q’’)\in T,\sigma\in\Sigma\rbrace\newline
\hspace{1cm} \cdot \ Acc’ = Acc
\end{array}$

Because the subtrees of a $\lbrace 1\rbrace$-labeled binary tree are the same from all nodes, we can simplify its acceptance game such that only finitely many positions are needed. We call this game the emptiness game.

$\textbf{Definition 12.5. } \text{Let }\mathcal{A}=(\Sigma,Q,q_0,T,Acc)\text{ be a tree automaton. The }\textit{emptiness game}\text{ of }\mathcal{A}$ $ \text{ is the game }\mathcal{G}_{\mathcal{A}}=(\mathcal{A}’,\text{Win}’)\text{ with the finite game arena }\mathcal{A}’=(Q\cup T, Q,T,E)\text{, where}$ $ E=\lbrace(q,\tau)\mid\tau=(q,\sigma,q^0,q^1),\tau\in T\rbrace\cup\lbrace(\tau,q’)\mid\tau=(\rule{0.5em}{0.4pt},\sigma,q^0,q^1)\text{ and }(q’=q^0\text{ or }q’=q^1)\rbrace$ $\text{and Win’}=\lbrace q(0)\tau(0)q(1)\tau(1)\dots\mid q(0)q(1)\dots\in Acc,\tau(0)\tau(1)\dots\in T^\omega\rbrace$

$\textbf{Theorem 12.2. } \textit{The language of a tree automaton }\mathcal{A}\textit{ is non-empty iff Player 0 wins the}$ $\textit{emptiness game }\mathcal{G}_{\mathcal{A}}\textit{ from position }q_0.$

Proof

The emptiness game corresponds to the acceptance game of the automaton from Construction 12.1 on the $\lbrace 1\rbrace$-labeled binary tree.

Previous chapter: A Remark on Undetermined Games

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

Infinite games allow us to reason elegantly about infinite trees. A famous example of an argument that became significantly simpler with the introduction of game-theoretic ideas is the proof of Rabin’s theorem.

Rabin’s theorem states that the satisfiability of monadic second-order logic with two successors (S2S) is decidable. Like in Section 6, where we showed that S1S formulas can be translated to automata, we will show that S2S formulas can be translated to automata, this time, in order to accommodate more than one successor function, to automata over infinite trees.

The most difficult part of the proof of Rabin’s theorem is to show that tree automata are closed under complement. The original proof was purely combinatorial (and very difficult to understand), but the game-theoretic argument is simply based on the determinacy of the acceptance game of the tree automaton:

• the acceptance of a tree by a tree automaton = the existence of a winning strategy for Player 0,

• the non-acceptance = the absence of such a strategy = the existence of a winning strategy for Player 1.

We can therefore complement the language of a given tree automaton by constructing a new automaton that verifies the existence of a winning strategy for Player 1. We begin this section with a discussion of tree automata. The logic S2S and the translation to tree automata will be introduced later in the section.

Tree Automata

We consider tree automata over infinite binary trees. We use the notation for trees introduced in Section 7.1. The (full) binary tree is the language $\mathcal{T} =\lbrace 0, 1\rbrace^\ast$. For an alphabet $\Sigma, \mathcal{T}_\Sigma = \lbrace(\mathcal{T}, t)\mid t:\mathcal{T}\rightarrow\Sigma\rbrace$ is the set of all binary $\Sigma$-labeled trees.

Previous chapter: Muller Games

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Since we have shown that reachability, Büchi, parity, and Muller games are all determined, it might seem as if all games were determined. The purpose of this last subsection is to remark that this is not the case. By definition, every play is either won by Player 0 or by Player 1; however, it is entirely possible that neither Player 0 nor Player 1 has a winning strategy.

We will construct a game with a winning condition that allows the players to steal strategies in the sense that if Player i has a winning strategy σ, then Player 1−$i$ has a strategy $\tau$ that mimicks $\sigma$ so that the play resulting from strategies σ and τ is won by Player 1-$i$: hence, strategy $\sigma$ is not winning after all!

We fix the alphabet $\mathbb{B}=\lbrace 0,1\rbrace$. To define the winning condition, we introduce an infinite $\text{XOR}$ function $f$. An infinite $\text{XOR}$ function is a function $f:\mathbb{B}^\omega\rightarrow\mathbb{B}$ such that $f(\alpha)\neq f(\beta)$ for all α, β ∈ B ω that have the exact same letter in every position except for exactly one position where they have different letters.

To see that such a function exists, define an equivalence relation $\sim$ such that $\alpha\sim\beta$ iff there exists a position $n\in\mathbb{N}$ such that $\alpha(i)=\beta(i)$ for all $i\geq n$. Let $S\subseteq\mathbb{B}^\omega$ be a set that contains exactly one element from each $\sim$-equivalence class, and let $r(\alpha)$ be the unique $\beta\in S$ such that $\alpha\sim\beta$. For every $\alpha\in\mathbb{B}^\omega$, the two sequences $\alpha$ and $r(\alpha)$ differ only in a finite number of positions. We define $f(\alpha)=0$ if this number is even and $f(\alpha)=1$ if it is odd. Hence, $f$ is indeed an infinite $\text{XOR}$ function: if two sequences $\alpha,\beta\in\mathbb{B}^\omega$ differ in exactly one position, then $f(\alpha)\neq f(\beta)$.

We now use the infinite $\text{XOR}$ function $f$ to define the game. We’ll describe the game somewhat informally in terms of rounds executed by the players; it is straightforward to translate this into an explicit arena and winning condition. Our game is played in rounds $n = 0, 1, 2,\dots,$ where in round $n$, first Player 0 picks a finite word $w_{2n}\in\mathbb{B}^+$, then Player 1 picks $w_{2n+1}\in\mathbb{B}^+$. The resulting play $\alpha=w_0,w_1,w_2,\dots$ is winning for Player $f(\alpha)$.

We now use the “strategy stealing” argument to show that no player has a winnig strategy in this game. A strategy for Player $i$ is a mapping $\sigma:\cup_{n\in\mathbb{N}}(\mathbb{B}^+)^{2n+i}$, where we denote $(\mathbb{B}^+)^0=\varepsilon$.

As usual, $\sigma$ is a winning strategy for Player $i$ if Player $i$ wins every play that is consistent with $\sigma_i$ . Now fix an arbitrary strategy $\tau$ for Player 1. From $\tau$, we construct two different strategies $\sigma$ and $\sigma’$ for Player 0.

For the first round:

Previous chapter: Parity Games

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Muller games differ from the games we have studied so far in that they are not memoryless determined. Consider, for example, a game arena consisting of three positions $v_0,v_1,v_2$, such that there are edges from $v_0$ and $v_2$ to $v_1$ and from $v_1$ to $v_0$ and $v_2$. Hence, the only choice in the game is in $v_1$, where Player 0 gets to choose between moving to $v_0$ or $v_2$:

The Muller condition $\mathcal{F}=\lbrace\lbrace v_0,v_1,v_2\rbrace\rbrace$ is only satisfied if all three positions are visited infinitely often. Player 0 can therefore not win the game with a memoryless strategy, because such a strategy would either visit $v_0$ and $v_1$ infinitely often, or $v_1$ and $v_2$, but not all three positions.

There is, however, a memoryful winning strategy: simply alternate between moving from $v_1$ to $v_0$ and to $v_2$.

In the following, we solve Muller games via a reduction to parity games, i.e., we define a parity game such that we can translate the winning strategy in the parity game into a winning strategy in the Muller game.

The fact that parity games are memoryless determined and Muller games are not, is not a contradiction: our reduction introduces additional state into the parity game, such that, on the extended state space, there exists a memoryless winning strategy. This augmentation of the state space is known as the latest appearence record:

Latest Appearence Record

$\textbf{Definition 11.11. } \text{Let }V\text{ be the set of positions of the game arena and let }{$}\text{ be some fresh}$ $\text{symbol. A }\textit{latest appearence record}\text{ over }V\text{ is a finite word over the alphabet }V\cup\lbrace{$}\rbrace\text{ where every}$ $\text{letter from }V\cup\lbrace{$}\rbrace\text{ appears exactly once and whose first letter is from }V\text{ . The }\textit{hit set}\text{ of a latest}$ $\text{appearence record }\ell=v_0v_1\dots v_m{$}v_m+1\dots v_n\text{ is defined as }hit(\ell)=\lbrace v_0,\dots v_m\rbrace.$

Previous chapter: Büchi Games

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Introduction

Perhaps the most intriguing type of infinite games are parity games. Parity games play a key role in verification (in particular for $\mu$-calculus model checking) and synthesis, and finding fast algorithms for parity games is an active research topic.

The algorithm discussed in the following takes exponential time. There are also several quasi-polynomial-time algorithms for solving parity games (starting with a breakthrough result by Calude, Jain, Khoussainov, Li, and Stephan in 2017). In practice, however, these algorithms do not perform well (yet).

Parity Condition

$\textbf{Definition 11.10. }\text{The }\textit{parity condition }\small\text{PARITY} \normalsize(C)\text{ for a coloring function }c:V\rightarrow\mathbb{N}\text{ is the set}$
$$\small\text{PARITY} \normalsize(C)=\lbrace\alpha\in V^\omega\mid\text{max}\lbrace c(q)\mid q\in\text{Inf}(\alpha)\rbrace\text{is even}\rbrace.$$

The parity condition is satisfied if the biggest number $q$ of the coloring function is even, among all positions that are visited infinitely often.

Example

Previous chapter: Reachability Games

This is a learning note of a course in CISPA, UdS. Taught by Bernd Finkbeiner

Recurrence Construction

In a Büchi game, the goal of Player 0 is to visit some accepting position infinitely often. The attractor construction checks whether there is a strategy which enforces at least one visit to an accepting position. Reaching an accepting state at least once is indeed a necessary precondition, but we also have to ensure that from this position we can enforce a second visit to some accepting state, then a third, and so forth.

The recurrence construction computes the largest subset of the accepting states from which Player 0 can enforce infinitely many subsequent visits to the subset.

$\textbf{Construction 11.2. } \text{Let an arena }\mathcal{A} = (V_0,V_1,E)\text{ with }V=V_0\cup V_1\text{ be given. The }$ $\textit{recurrence construction}\text{ on }\mathcal{A}\text{ is defined for all }n\in\mathbb{N}\text{ and }F\subseteq V\text{ as:}$
$\begin{array}{lll} \hspace{1cm} \cdot \ W_n^1(F) &=& V\setminus Attr^0(Recur_n(F))\newline \hspace{1cm} \cdot \ Recur_{0}(F)&=&F \newline \hspace{1cm} \cdot \ Recur_{n+1}(F)&=&Recur_{n}(F)\setminus CPre^{1}(W_n^1(F)) \newline \hspace{1cm} \cdot \ Recur(F)&=&\underset{n\in\mathbb{N}}{\bigcap} Recur_{n}(R)\newline \end{array}$

The set $W_n^1(F)$ contains those positions in $V$ from which Player 1 can enforce that at most $n$ visits to $F$.

The set $CPre^{1}(W_n^1(F))$ adds those positions in $V$ from which move to positions in $W_n^1(F)$, meaning that there are at most $n+1$ visits to $F$ in newly added positions.

The set $Recur_{n}(F)$ contains the subset of $F$ from which Player 0 can enforce at least $n$ further (i.e., a total of at least $n+1$) visits to $F$.

The set $Recur(F)$ contains the subset of $F$ from which Player 0 can enforce infinitely many visits to $F$. The recurrence construction solves a game with winning condition $\small\text{BÜCHI} \normalsize (F)$ as follows: